18. The Aiyagari Model#

GPU

This lecture was built using a machine with JAX installed and access to a GPU.

To run this lecture on Google Colab, click on the “play” icon top right, select Colab, and set the runtime environment to include a GPU.

To run this lecture on your own machine, you need to install Google JAX.

18.1. Overview#

In this lecture, we describe the structure of a class of models that build on work by Truman Bewley [Bew77].

We begin by discussing an example of a Bewley model due to Rao Aiyagari [Aiy94].

The model features

  • Heterogeneous agents

  • A single exogenous vehicle for borrowing and lending

  • Limits on amounts individual agents may borrow

The Aiyagari model has been used to investigate many topics, including

  • precautionary savings and the effect of liquidity constraints [Aiy94]

  • risk sharing and asset pricing [HL96]

  • the shape of the wealth distribution [BBZ15]

18.1.1. References#

The primary reference for this lecture is [Aiy94].

A textbook treatment is available in chapter 18 of [LS18].

A less sophisticated version of this lecture (without JAX) can be found here.

18.1.2. Preliminaries#

We use the following imports

import time
import matplotlib.pyplot as plt
import numpy as np
import jax
import jax.numpy as jnp
from collections import namedtuple

Let’s check the GPU we are running

!nvidia-smi

Tue Apr 29 04:37:04 2025       
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 570.133.20             Driver Version: 570.133.20     CUDA Version: 12.8     |
|-----------------------------------------+------------------------+----------------------+
| GPU  Name                 Persistence-M | Bus-Id          Disp.A | Volatile Uncorr. ECC |
| Fan  Temp   Perf          Pwr:Usage/Cap |           Memory-Usage | GPU-Util  Compute M. |
|                                         |                        |               MIG M. |
|=========================================+========================+======================|
|   0  Tesla T4                       Off |   00000000:00:1E.0 Off |                    0 |
| N/A   25C    P8             13W /   70W |       0MiB /  15360MiB |      0%      Default |
|                                         |                        |                  N/A |
+-----------------------------------------+------------------------+----------------------+
                                                                                         
+-----------------------------------------------------------------------------------------+
| Processes:                                                                              |
|  GPU   GI   CI              PID   Type   Process name                        GPU Memory |
|        ID   ID                                                               Usage      |
|=========================================================================================|
|  No running processes found                                                             |
+-----------------------------------------------------------------------------------------+

We will use 64 bit floats with JAX in order to increase the precision.

jax.config.update("jax_enable_x64", True)

We will use the following function to compute stationary distributions of stochastic matrices. (For a reference to the algorithm, see p. 88 of Economic Dynamics.)

@jax.jit
def compute_stationary(P):
    n = P.shape[0]
    I = jnp.identity(n)
    O = jnp.ones((n, n))
    A = I - jnp.transpose(P) + O
    return jnp.linalg.solve(A, jnp.ones(n))

18.2. Firms#

Firms produce output by hiring capital and labor.

Firms act competitively and face constant returns to scale.

Since returns to scale are constant the number of firms does not matter.

Hence we can consider a single (but nonetheless competitive) representative firm.

The firm’s output is

\[ Y = A K^{\alpha} N^{1 - \alpha} \]

where

  • \( A \) and \( \alpha \) are parameters with \( A > 0 \) and \( \alpha \in (0, 1) \)

  • \( K\) is aggregate capital

  • \( N \) is total labor supply (which is constant in this simple version of the model)

The firm’s problem is

\[ \max_{K, N} \left\{ A K^{\alpha} N^{1 - \alpha} - (r + \delta) K - w N \right\} \]

The parameter \( \delta \) is the depreciation rate.

These parameters are stored in the following namedtuple.

Firm = namedtuple('Firm', ('A', 'N', 'α', 'δ'))

def create_firm(A=1.0,
                N=1.0,
                α=0.33,
                δ=0.05):
    """
    Create a namedtuple that stores firm data.
    
    """
    return Firm(A=A, N=N, α=α, δ=δ)

From the first-order condition with respect to capital, the firm’s inverse demand for capital is

(18.1)#\[r = A \alpha \left( \frac{N}{K} \right)^{1 - \alpha} - \delta\]
def r_given_k(K, firm):
    """
    Inverse demand curve for capital.  The interest rate associated with a
    given demand for capital K.
    """
    A, N, α, δ = firm
    return A * α * (N / K)**(1 - α) - δ

Using (18.1) and the firm’s first-order condition for labor,

(18.2)#\[w(r) = A (1 - \alpha) (A \alpha / (r + \delta))^{\alpha / (1 - \alpha)}\]
def r_to_w(r, firm):
    """
    Equilibrium wages associated with a given interest rate r.
    """
    A, N, α, δ = firm
    return A * (1 - α) * (A * α / (r + δ))**(α / (1 - α))

18.3. Households#

Infinitely lived households / consumers face idiosyncratic income shocks.

A unit interval of ex-ante identical households face a common borrowing constraint.

The savings problem faced by a typical household is

\[ \max \mathbb E \sum_{t=0}^{\infty} \beta^t u(c_t) \]

subject to

\[ a_{t+1} + c_t \leq w z_t + (1 + r) a_t \quad c_t \geq 0, \quad \text{and} \quad a_t \geq -B \]

where

  • \( c_t \) is current consumption

  • \( a_t \) is assets

  • \( z_t \) is an exogenous component of labor income capturing stochastic unemployment risk, etc.

  • \( w \) is a wage rate

  • \( r \) is a net interest rate

  • \( B \) is the maximum amount that the agent is allowed to borrow

The exogenous process \( \{z_t\} \) follows a finite state Markov chain with given stochastic matrix \( P \).

In this simple version of the model, households supply labor inelastically because they do not value leisure.

Below we provide code to solve the household problem, taking \(r\) and \(w\) as fixed.

18.3.1. Primitives and Operators#

We will solve the household problem using Howard policy iteration (see Ch 5 of Dynamic Programming).

First we set up a namedtuple to store the parameters that define a household asset accumulation problem, as well as the grids used to solve it.

Household = namedtuple('Household', 
                       ('β', 'a_grid', 'z_grid', 'Π'))

def create_household(β=0.96,                      # Discount factor
                     Π=[[0.9, 0.1], [0.1, 0.9]],  # Markov chain
                     z_grid=[0.1, 1.0],           # Exogenous states
                     a_min=1e-10, a_max=20,       # Asset grid
                     a_size=200):
    """
    Create a namedtuple that stores all data needed to solve the household
    problem, given prices.

    """
    a_grid = jnp.linspace(a_min, a_max, a_size)
    z_grid, Π = map(jnp.array, (z_grid, Π))
    return Household(β=β, a_grid=a_grid, z_grid=z_grid, Π=Π)

For now we assume that \(u(c) = \log(c)\).

(CRRA utility is treated in the exercises.)

u = jnp.log

Here’s a tuple that stores the wage rate and interest rate, as well as a function that creates a price namedtuple with default values.

Prices = namedtuple('Prices', ('r', 'w'))

def create_prices(r=0.01,   # Interest rate
                  w=1.0):   # Wages
    return Prices(r=r, w=w)

Now we set up a vectorized version of the right-hand side of the Bellman equation (before maximization), which is a 3D array representing

\[ B(a, z, a') = u(wz + (1+r)a - a') + \beta \sum_{z'} v(a', z') Π(z, z') \]

for all \((a, z, a')\).

@jax.jit
def B(v, household, prices):
    # Unpack
    β, a_grid, z_grid, Π = household
    a_size, z_size = len(a_grid), len(z_grid)
    r, w = prices

    # Compute current consumption as array c[i, j, ip]
    a  = jnp.reshape(a_grid, (a_size, 1, 1))    # a[i]   ->  a[i, j, ip]
    z  = jnp.reshape(z_grid, (1, z_size, 1))    # z[j]   ->  z[i, j, ip]
    ap = jnp.reshape(a_grid, (1, 1, a_size))    # ap[ip] -> ap[i, j, ip]
    c = w * z + (1 + r) * a - ap

    # Calculate continuation rewards at all combinations of (a, z, ap)
    v = jnp.reshape(v, (1, 1, a_size, z_size))  # v[ip, jp] -> v[i, j, ip, jp]
    Π = jnp.reshape(Π, (1, z_size, 1, z_size))  # Π[j, jp]  -> Π[i, j, ip, jp]
    EV = jnp.sum(v * Π, axis=-1)                 # sum over last index jp

    # Compute the right-hand side of the Bellman equation
    return jnp.where(c > 0, u(c) + β * EV, -jnp.inf)

The next function computes greedy policies.

@jax.jit
def get_greedy(v, household, prices):
    """
    Computes a v-greedy policy σ, returned as a set of indices.  If 
    σ[i, j] equals ip, then a_grid[ip] is the maximizer at i, j.

    """
    return jnp.argmax(B(v, household, prices), axis=-1) # argmax over ap

The following function computes the array \(r_{\sigma}\) which gives current rewards given policy \(\sigma\).

@jax.jit
def compute_r_σ(σ, household, prices):
    """
    Compute current rewards at each i, j under policy σ.  In particular,

        r_σ[i, j] = u((1 + r)a[i] + wz[j] - a'[ip])

    when ip = σ[i, j].

    """
    # Unpack
    β, a_grid, z_grid, Π = household
    a_size, z_size = len(a_grid), len(z_grid)
    r, w = prices

    # Compute r_σ[i, j]
    a = jnp.reshape(a_grid, (a_size, 1))
    z = jnp.reshape(z_grid, (1, z_size))
    ap = a_grid[σ]
    c = (1 + r) * a + w * z - ap
    r_σ = u(c)

    return r_σ

The value \(v_{\sigma}\) of a policy \(\sigma\) is defined as

\[ v_{\sigma} = (I - \beta P_{\sigma})^{-1} r_{\sigma} \]

(See Ch 5 of Dynamic Programming for notation and background on Howard policy iteration.)

To compute this vector, we set up the linear map \(v \rightarrow R_{\sigma} v\), where \(R_{\sigma} := I - \beta P_{\sigma}\).

This map can be expressed as

\[ (R_{\sigma} v)(a, z) = v(a, z) - \beta \sum_{z'} v(\sigma(a, z), z') Π(z, z') \]

(Notice that \(R_\sigma\) is expressed as a linear operator rather than a matrix – this is much easier and cleaner to code, and also exploits sparsity.)

@jax.jit
def R_σ(v, σ, household):
    # Unpack
    β, a_grid, z_grid, Π = household
    a_size, z_size = len(a_grid), len(z_grid)

    # Set up the array v[σ[i, j], jp]
    zp_idx = jnp.arange(z_size)
    zp_idx = jnp.reshape(zp_idx, (1, 1, z_size))
    σ = jnp.reshape(σ, (a_size, z_size, 1))
    V = v[σ, zp_idx]
    
    # Expand Π[j, jp] to Π[i, j, jp]
    Π = jnp.reshape(Π, (1, z_size, z_size))
    
    # Compute and return v[i, j] - β Σ_jp v[σ[i, j], jp] * Π[j, jp]
    return v - β * jnp.sum(V * Π, axis=-1)

The next function computes the lifetime value of a given policy.

@jax.jit
def get_value(σ, household, prices):
    """
    Get the lifetime value of policy σ by computing

        v_σ = R_σ^{-1} r_σ

    """
    r_σ = compute_r_σ(σ, household, prices)
    # Reduce R_σ to a function in v
    _R_σ = lambda v: R_σ(v, σ, household)
    # Compute v_σ = R_σ^{-1} r_σ using an iterative routing.
    return jax.scipy.sparse.linalg.bicgstab(_R_σ, r_σ)[0]

Here’s the Howard policy iteration.

def howard_policy_iteration(household, prices,
                            tol=1e-4, max_iter=10_000, verbose=False):
    """
    Howard policy iteration routine.

    """
    β, a_grid, z_grid, Π = household
    a_size, z_size = len(a_grid), len(z_grid)
    σ = jnp.zeros((a_size, z_size), dtype=int)
    
    v_σ = get_value(σ, household, prices)
    i = 0
    error = tol + 1
    while error > tol and i < max_iter:
        σ_new = get_greedy(v_σ, household, prices)
        v_σ_new = get_value(σ_new, household, prices)
        error = jnp.max(jnp.abs(v_σ_new - v_σ))
        σ = σ_new
        v_σ = v_σ_new
        i = i + 1
        if verbose:
            print(f"Concluded loop {i} with error {error}.")
    return σ

As a first example of what we can do, let’s compute and plot an optimal accumulation policy at fixed prices.

# Create an instance of Household
household = create_household()
prices = create_prices()

r, w = prices

r, w

(0.01, 1.0)

%time σ_star = howard_policy_iteration(household, prices, verbose=True)

Concluded loop 1 with error 11.366831579022996.
Concluded loop 2 with error 9.574522771860245.
Concluded loop 3 with error 3.9654760004604777.
Concluded loop 4 with error 1.1207075306313232.
Concluded loop 5 with error 0.2524013153055833.
Concluded loop 6 with error 0.12172293662906064.
Concluded loop 7 with error 0.043395682867316765.
Concluded loop 8 with error 0.012132319676439351.
Concluded loop 9 with error 0.005822155404443308.
Concluded loop 10 with error 0.002863165320343697.
Concluded loop 11 with error 0.0016657175376657563.
Concluded loop 12 with error 0.0004143776102245589.
Concluded loop 13 with error 0.0.
CPU times: user 721 ms, sys: 100 ms, total: 822 ms
Wall time: 1.01 s

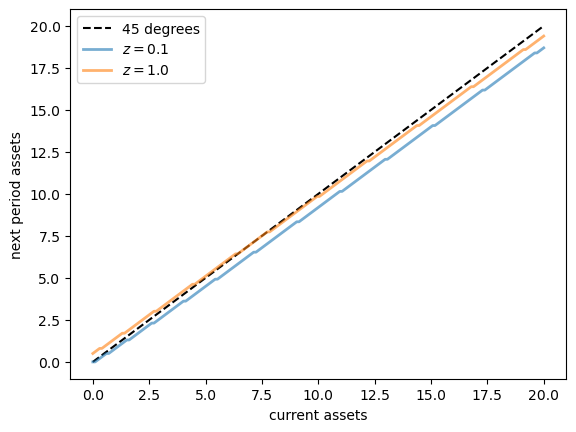
The next plot shows asset accumulation policies at different values of the exogenous state.

β, a_grid, z_grid, Π = household

fig, ax = plt.subplots()
ax.plot(a_grid, a_grid, 'k--', label="45 degrees")  
for j, z in enumerate(z_grid):
    lb = f'$z = {z:.2}$'
    policy_vals = a_grid[σ_star[:, j]]
    ax.plot(a_grid, policy_vals, lw=2, alpha=0.6, label=lb)
    ax.set_xlabel('current assets')
    ax.set_ylabel('next period assets')
ax.legend(loc='upper left')
plt.show()
_images/8b4fcf9be579643e39a3bcfe5fdcd76d1a9e2876ef72c0ce27ca401b2345d021.png

18.3.2. Capital Supply#

To start thinking about equilibrium, we need to know how much capital households supply at a given interest rate \(r\).

This quantity can be calculated by taking the stationary distribution of assets under the optimal policy and computing the mean.

The next function computes the stationary distribution for a given policy \(\sigma\) via the following steps:

  • compute the stationary distribution \(\psi = (\psi(a, z))\) of \(P_{\sigma}\), which defines the Markov chain of the state \((a_t, z_t)\) under policy \(\sigma\).

  • sum out \(z_t\) to get the marginal distribution for \(a_t\).

@jax.jit
def compute_asset_stationary(σ, household):
    # Unpack
    β, a_grid, z_grid, Π = household
    a_size, z_size = len(a_grid), len(z_grid)

    # Construct P_σ as an array of the form P_σ[i, j, ip, jp]
    ap_idx = jnp.arange(a_size)
    ap_idx = jnp.reshape(ap_idx, (1, 1, a_size, 1))
    σ = jnp.reshape(σ, (a_size, z_size, 1, 1))
    A = jnp.where(σ == ap_idx, 1, 0)
    Π = jnp.reshape(Π, (1, z_size, 1, z_size))
    P_σ = A * Π

    # Reshape P_σ into a matrix
    n = a_size * z_size
    P_σ = jnp.reshape(P_σ, (n, n))

    # Get stationary distribution and reshape back onto [i, j] grid
    ψ = compute_stationary(P_σ)
    ψ = jnp.reshape(ψ, (a_size, z_size))

    # Sum along the rows to get the marginal distribution of assets
    ψ_a = jnp.sum(ψ, axis=1)
    return ψ_a

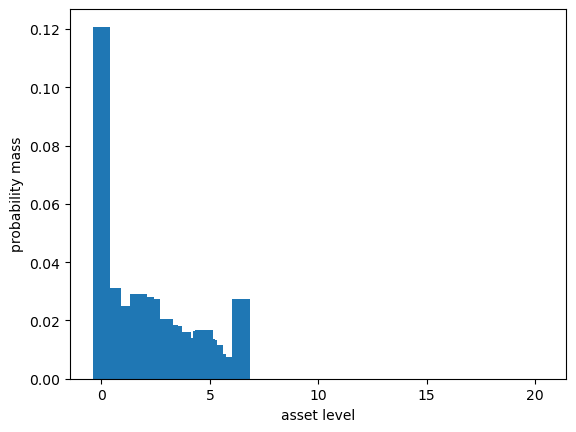
Let’s give this a test run.

ψ_a = compute_asset_stationary(σ_star, household)

fig, ax = plt.subplots()
ax.bar(household.a_grid, ψ_a)
ax.set_xlabel("asset level")
ax.set_ylabel("probability mass")
plt.show()
_images/c7f36637c90af01db94cfaa7eeca048f5ba70d2739974a2aa9faadda766614fd.png

The distribution should sum to one:

ψ_a.sum()

Array(1., dtype=float64)

The next function computes aggregate capital supply by households under policy \(\sigma\), given wages and interest rates.

def capital_supply(σ, household):
    """
    Induced level of capital stock under the policy, taking r and w as given.
    
    """
    β, a_grid, z_grid, Π = household
    ψ_a = compute_asset_stationary(σ, household)
    return float(jnp.sum(ψ_a * a_grid))

18.4. Equilibrium#

We compute a stationary rational expectations equilibrium (SREE) as follows:

  1. set \(n=0\), start with initial guess \( K_0\) for aggregate capital

  2. determine prices \(r, w\) from the firm decision problem, given \(K_n\)

  3. compute the optimal savings policy of the households given these prices

  4. compute aggregate capital \(K_{n+1}\) as the mean of steady state capital given this savings policy

  5. if \(K_{n+1} \approx K_n\) stop, otherwise go to step 2.

We can write the sequence of operations in steps 2-4 as

\[ K_{n + 1} = G(K_n) \]

If \(K_{n+1}\) agrees with \(K_n\) then we have a SREE.

In other words, our problem is to find the fixed-point of the one-dimensional map \(G\).

Here’s \(G\) expressed as a Python function:

def G(K, firm, household):
    # Get prices r, w associated with K
    r = r_given_k(K, firm)
    w = r_to_w(r, firm)
    # Generate a household object with these prices, compute
    # aggregate capital.
    prices = create_prices(r=r, w=w)
    σ_star = howard_policy_iteration(household, prices)
    return capital_supply(σ_star, household)

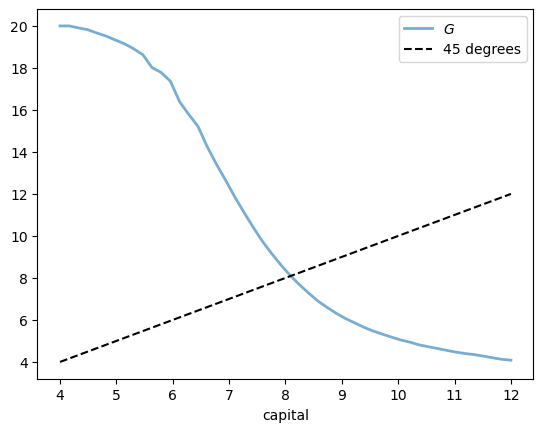
18.4.1. Visual inspection#

Let’s inspect visually as a first pass.

num_points = 50
firm = create_firm()
household = create_household()
k_vals = np.linspace(4, 12, num_points)
out = [G(k, firm, household) for k in k_vals]

fig, ax = plt.subplots()
ax.plot(k_vals, out, lw=2, alpha=0.6, label='$G$')
ax.plot(k_vals, k_vals, 'k--', label="45 degrees")
ax.set_xlabel('capital')
ax.legend()
plt.show()
_images/00a3ff68b5e460c630093ef7f961be91bc5eb4cfe0b9b32dc7d22d87854d46d4.png

18.4.2. Computing the equilibrium#

Now let’s compute the equilibrium.

Looking at the figure above, we see that a simple iteration scheme \(K_{n+1} = G(K_n)\) will cycle from high to low values, leading to slow convergence.

As a result, we use a damped iteration scheme of the form

\[ K_{n+1} = \alpha K_n + (1-\alpha) G(K_n) \]
def compute_equilibrium(firm, household,
                        K0=6, α=0.99, max_iter=1_000, tol=1e-4, 
                        print_skip=10, verbose=False):
    n = 0
    K = K0
    error = tol + 1
    while error > tol and n < max_iter:
        new_K = α * K + (1 - α) * G(K, firm, household)
        error = abs(new_K - K)
        K = new_K
        n += 1
        if verbose and n % print_skip == 0:
            print(f"At iteration {n} with error {error}")
    return K, n

firm = create_firm()
household = create_household()
print("\nComputing equilibrium capital stock")
start = time.time()
K_star, n = compute_equilibrium(firm, household, K0=6.0, verbose=True)
elapsed = time.time() - start
print(f"Computed equilibrium {K_star:.5} in {n} iterations and {elapsed} seconds")

Computing equilibrium capital stock

At iteration 10 with error 0.06490545798825043

At iteration 20 with error 0.03626685465742874

At iteration 30 with error 0.021452703682580676

At iteration 40 with error 0.013383829253038826

At iteration 50 with error 0.008397515264451982

At iteration 60 with error 0.005656370053102933

At iteration 70 with error 0.003750107819944226

At iteration 80 with error 0.0024816210955460605

At iteration 90 with error 0.0017352118525710836

At iteration 100 with error 0.0009559876839571047

At iteration 110 with error 0.0006843412658508186

At iteration 120 with error 0.00046762845631675987

At iteration 130 with error 0.00038193101011607666

At iteration 140 with error 0.00019421626809901227

At iteration 150 with error 0.00017041810881579522

At iteration 160 with error 0.00015412308287032772

At iteration 170 with error 0.00013938615349395889

Computed equilibrium 8.0918 in 176 iterations and 37.21316719055176 seconds

This is not very fast, given how quickly we can solve the household problem.

You can try varying \(\alpha\), but usually this parameter is hard to set a priori.

In the exercises below you will be asked to use bisection instead, which generally performs better.

18.5. Exercises#

Exercise 18.1

Write a new version of compute_equilibrium that uses bisect from scipy.optimize instead of damped iteration.

See if you can make it faster that the previous version.

In bisect,

  • you should set xtol=1e-4 to have the same error tolerance as the previous version.

  • for the lower and upper bounds of the bisection routine try a = 1.0 and b = 20.0.

Exercise 18.2

Show how equilibrium capital stock changes with \(\beta\).

Use the following values of \(\beta\) and plot the relationship you find.

β_vals = np.linspace(0.94, 0.98, 20)