16. Endogenous Grid Method#
GPU
This lecture was built using a machine with JAX installed and access to a GPU.
To run this lecture on Google Colab, click on the “play” icon top right, select Colab, and set the runtime environment to include a GPU.
To run this lecture on your own machine, you need to install Google JAX.
16.1. Overview#
In this lecture we use the endogenous grid method (EGM) to solve a basic income fluctuation (optimal savings) problem.
Background on the endogenous grid method can be found in an earlier QuantEcon lecture.
Here we focus on providing an efficient JAX implementation.
In addition to JAX and Anaconda, this lecture will need the following libraries:
!pip install --upgrade quantecon
Show code cell output
Requirement already satisfied: quantecon in /opt/conda/envs/quantecon/lib/python3.12/site-packages (0.7.2)
Requirement already satisfied: numba>=0.49.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (0.60.0)
Requirement already satisfied: numpy>=1.17.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.26.4)
Requirement already satisfied: requests in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (2.32.3)
Requirement already satisfied: scipy>=1.5.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.13.1)
Requirement already satisfied: sympy in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.13.2)
Requirement already satisfied: llvmlite<0.44,>=0.43.0dev0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from numba>=0.49.0->quantecon) (0.43.0)
Requirement already satisfied: charset-normalizer<4,>=2 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (3.3.2)
Requirement already satisfied: idna<4,>=2.5 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (3.7)
Requirement already satisfied: urllib3<3,>=1.21.1 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (2.2.3)
Requirement already satisfied: certifi>=2017.4.17 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (2024.8.30)
Requirement already satisfied: mpmath<1.4,>=1.1.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from sympy->quantecon) (1.3.0)
WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager, possibly rendering your system unusable.It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv. Use the --root-user-action option if you know what you are doing and want to suppress this warning.
import quantecon as qe
import matplotlib.pyplot as plt
import numpy as np
import jax
import jax.numpy as jnp
import numba
from time import time
Let’s check the GPU we are running
!nvidia-smi
Tue Nov 19 23:55:35 2024
+---------------------------------------------------------------------------------------+
| NVIDIA-SMI 535.54.03 Driver Version: 535.54.03 CUDA Version: 12.6 |
|-----------------------------------------+----------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+======================+======================|
| 0 Tesla T4 On | 00000001:00:00.0 Off | 0 |
| N/A 44C P0 28W / 70W | 2MiB / 15360MiB | 0% Default |
| | | N/A |
+-----------------------------------------+----------------------+----------------------+
+---------------------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=======================================================================================|
| No running processes found |
+---------------------------------------------------------------------------------------+
We use 64 bit floating point numbers for extra precision.
jax.config.update("jax_enable_x64", True)
16.2. Setup#
We consider a household that chooses a state-contingent consumption plan \(\{c_t\}_{t \geq 0}\) to maximize
subject to
Here \(R = 1 + r\) where \(r\) is the interest rate.
The income process \(\{Y_t\}\) is a Markov chain generated by stochastic matrix \(P\).
The matrix \(P\) and the grid of values taken by \(Y_t\) are obtained by discretizing the AR(1) process
where \(\{\epsilon_t\}\) is IID and standard normal.
Utility has the CRRA specification
The following function stores default parameter values for the income fluctuation problem and creates suitable arrays.
def ifp(R=1.01, # gross interest rate
β=0.99, # discount factor
γ=1.5, # CRRA preference parameter
s_max=16, # savings grid max
s_size=200, # savings grid size
ρ=0.99, # income persistence
ν=0.02, # income volatility
y_size=25): # income grid size
# require R β < 1 for convergence
assert R * β < 1, "Stability condition failed."
# Create income Markov chain
mc = qe.tauchen(y_size, ρ, ν)
y_grid, P = jnp.exp(mc.state_values), mc.P
# Shift to JAX arrays
P, y_grid = jax.device_put((P, y_grid))
s_grid = jnp.linspace(0, s_max, s_size)
# Pack and return
constants = β, R, γ
sizes = s_size, y_size
arrays = s_grid, y_grid, P
return constants, sizes, arrays
16.3. Solution method#
Let \(S = \mathbb R_+ \times \mathsf Y\) be the set of possible values for the state \((a_t, Y_t)\).
We aim to compute an optimal consumption policy \(\sigma^* \colon S \to \mathbb R\), under which dynamics are given by
In this section we discuss how we intend to solve for this policy.
16.3.1. Euler equation#
The Euler equation for the optimization problem is
An explanation for this expression can be found here.
We rewrite the Euler equation in functional form
where \((u' \circ \sigma)(a, y) := u'(\sigma(a, y))\) and \(\sigma\) is a consumption policy.
For given consumption policy \(\sigma\), we define \((K \sigma) (a,y)\) as the unique \(c \in [0, a]\) that solves
iterating with \(K\) computes an optimal policy and
if \(\sigma\) is increasing in its first argument, then so is \(K\sigma\)
Hence below we always assume that \(\sigma\) is increasing in its first argument.
The EGM is a technique for computing the update \(K\sigma\) given \(\sigma\) along a grid of asset values.
Notice that, since \(u'(a) \to \infty\) as \(a \downarrow 0\), the second term in the max in (16.1) dominates for sufficiently small \(a\).
Also, again using (16.1), we have \(c=a\) for all such \(a\).
Hence, for sufficiently small \(a\),
Equality holds at \(\bar a(y)\) given by
We can now write
Equivalently, we can state that the \(c\) satisfying \(c = (K\sigma)(a, y)\) obeys
We begin with an exogenous grid of saving values \(0 = s_0 < \ldots < s_{N-1}\)
Using the exogenous savings grid, and a fixed value of \(y\), we create an endogenous asset grid \(a_0, \ldots, a_{N-1}\) and a consumption grid \(c_0, \ldots, c_{N-1}\) as follows.
First we set \(a_0 = c_0 = 0\), since zero consumption is an optimal (in fact the only) choice when \(a=0\).
Then, for \(i > 0\), we compute
and we set
We claim that each pair \(a_i, c_i\) obeys (16.2).
Indeed, since \(s_i > 0\), choosing \(c_i\) according to (16.3) gives
where the inequality uses the fact that \(\sigma\) is increasing in its first argument.
If we now take \(a_i = s_i + c_i\) we get \(a_i > \bar a(y)\), so the pair \((a_i, c_i)\) satisfies
Hence (16.2) holds.
We are now ready to iterate with \(K\).
16.3.2. JAX version#
First we define a vectorized operator \(K\) based on the EGM.
Notice in the code below that
we avoid all loops and any mutation of arrays
the function is pure (no globals, no mutation of inputs)
def K_egm(a_in, σ_in, constants, sizes, arrays):
"""
The vectorized operator K using EGM.
"""
# Unpack
β, R, γ = constants
s_size, y_size = sizes
s_grid, y_grid, P = arrays
def u_prime(c):
return c**(-γ)
def u_prime_inv(u):
return u**(-1/γ)
# Linearly interpolate σ(a, y)
def σ(a, y):
return jnp.interp(a, a_in[:, y], σ_in[:, y])
σ_vec = jnp.vectorize(σ)
# Broadcast and vectorize
y_hat = jnp.reshape(y_grid, (1, 1, y_size))
y_hat_idx = jnp.reshape(jnp.arange(y_size), (1, 1, y_size))
s = jnp.reshape(s_grid, (s_size, 1, 1))
P = jnp.reshape(P, (1, y_size, y_size))
# Evaluate consumption choice
a_next = R * s + y_hat
σ_next = σ_vec(a_next, y_hat_idx)
up = u_prime(σ_next)
E = jnp.sum(up * P, axis=-1)
c = u_prime_inv(β * R * E)
# Set up a column vector with zero in the first row and ones elsewhere
e_0 = jnp.ones(s_size) - jnp.identity(s_size)[:, 0]
e_0 = jnp.reshape(e_0, (s_size, 1))
# The policy is computed consumption with the first row set to zero
σ_out = c * e_0
# Compute a_out by a = s + c
a_out = np.reshape(s_grid, (s_size, 1)) + σ_out
return a_out, σ_out
Then we use jax.jit to compile \(K\).
We use static_argnums to allow a recompile whenever sizes changes, since the compiler likes to specialize on shapes.
K_egm_jax = jax.jit(K_egm, static_argnums=(3,))
Next we define a successive approximator that repeatedly applies \(K\).
def successive_approx_jax(model,
tol=1e-5,
max_iter=100_000,
verbose=True,
print_skip=25):
# Unpack
constants, sizes, arrays = model
β, R, γ = constants
s_size, y_size = sizes
s_grid, y_grid, P = arrays
# Initial condition is to consume all in every state
σ_init = jnp.repeat(s_grid, y_size)
σ_init = jnp.reshape(σ_init, (s_size, y_size))
a_init = jnp.copy(σ_init)
a_vec, σ_vec = a_init, σ_init
i = 0
error = tol + 1
while i < max_iter and error > tol:
a_new, σ_new = K_egm_jax(a_vec, σ_vec, constants, sizes, arrays)
error = jnp.max(jnp.abs(σ_vec - σ_new))
i += 1
if verbose and i % print_skip == 0:
print(f"Error at iteration {i} is {error}.")
a_vec, σ_vec = jnp.copy(a_new), jnp.copy(σ_new)
if error > tol:
print("Failed to converge!")
else:
print(f"\nConverged in {i} iterations.")
return a_new, σ_new
16.3.3. Numba version#
Below we provide a second set of code, which solves the same model with Numba.
The purpose of this code is to cross-check our results from the JAX version, as well as to do a runtime comparison.
Most readers will want to skip ahead to the next section, where we solve the model and run the cross-check.
@numba.jit
def K_egm_nb(a_in, σ_in, constants, sizes, arrays):
"""
The operator K using Numba.
"""
# Simplify names
β, R, γ = constants
s_size, y_size = sizes
s_grid, y_grid, P = arrays
def u_prime(c):
return c**(-γ)
def u_prime_inv(u):
return u**(-1/γ)
# Linear interpolation of policy using endogenous grid
def σ(a, z):
return np.interp(a, a_in[:, z], σ_in[:, z])
# Allocate memory for new consumption array
σ_out = np.zeros_like(σ_in)
a_out = np.zeros_like(σ_out)
for i, s in enumerate(s_grid[1:]):
i += 1
for z in range(y_size):
expect = 0.0
for z_hat in range(y_size):
expect += u_prime(σ(R * s + y_grid[z_hat], z_hat)) * \
P[z, z_hat]
c = u_prime_inv(β * R * expect)
σ_out[i, z] = c
a_out[i, z] = s + c
return a_out, σ_out
def successive_approx_numba(model, # Class with model information
tol=1e-5,
max_iter=100_000,
verbose=True,
print_skip=25):
# Unpack
constants, sizes, arrays = model
s_size, y_size = sizes
# make NumPy versions of arrays
arrays = tuple(map(np.array, arrays))
s_grid, y_grid, P = arrays
σ_init = np.repeat(s_grid, y_size)
σ_init = np.reshape(σ_init, (s_size, y_size))
a_init = np.copy(σ_init)
a_vec, σ_vec = a_init, σ_init
# Set up loop
i = 0
error = tol + 1
while i < max_iter and error > tol:
a_new, σ_new = K_egm_nb(a_vec, σ_vec, constants, sizes, arrays)
error = np.max(np.abs(σ_vec - σ_new))
i += 1
if verbose and i % print_skip == 0:
print(f"Error at iteration {i} is {error}.")
a_vec, σ_vec = np.copy(a_new), np.copy(σ_new)
if error > tol:
print("Failed to converge!")
else:
print(f"\nConverged in {i} iterations.")
return a_new, σ_new
16.4. Solutions#
Here we solve the IFP with JAX and Numba.
We will compare both the outputs and the execution time.
16.4.1. Outputs#
model = ifp()
Here’s a first run of the JAX code.
%%time
a_star_egm_jax, σ_star_egm_jax = successive_approx_jax(model,
print_skip=1000)
Error at iteration 1000 is 6.472028596182788e-05.
Error at iteration 2000 is 1.2994575430580468e-05.
Converged in 2192 iterations.
CPU times: user 3.04 s, sys: 793 ms, total: 3.83 s
Wall time: 2.5 s
Next let’s solve the same IFP with Numba.
%%time
a_star_egm_nb, σ_star_egm_nb = successive_approx_numba(model,
print_skip=1000)
Error at iteration 1000 is 6.472028596182788e-05.
Error at iteration 2000 is 1.2994575430802513e-05.
Converged in 2192 iterations.
CPU times: user 54.6 s, sys: 17.6 ms, total: 54.6 s
Wall time: 54.6 s
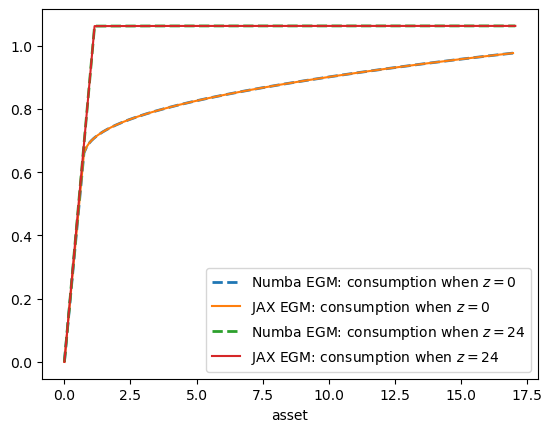
Now let’s check the outputs in a plot to make sure they are the same.
constants, sizes, arrays = model
β, R, γ = constants
s_size, y_size = sizes
s_grid, y_grid, P = arrays
fig, ax = plt.subplots()
for z in (0, y_size-1):
ax.plot(a_star_egm_nb[:, z],
σ_star_egm_nb[:, z],
'--', lw=2,
label=f"Numba EGM: consumption when $z={z}$")
ax.plot(a_star_egm_jax[:, z],
σ_star_egm_jax[:, z],
label=f"JAX EGM: consumption when $z={z}$")
ax.set_xlabel('asset')
plt.legend()
plt.show()
16.4.2. Timing#
Now let’s compare execution time of the two methods.
start = time()
a_star_egm_jax, σ_star_egm_jax = successive_approx_jax(model,
print_skip=1000)
jax_time_without_compile = time() - start
print("Jax execution time = ", jax_time_without_compile)
Error at iteration 1000 is 6.472028596182788e-05.
Error at iteration 2000 is 1.2994575430580468e-05.
Converged in 2192 iterations.
Jax execution time = 1.924191951751709
start = time()
a_star_egm_nb, σ_star_egm_nb = successive_approx_numba(model,
print_skip=1000)
numba_time_without_compile = time() - start
print("Numba execution time = ", numba_time_without_compile)
Error at iteration 1000 is 6.472028596182788e-05.
Error at iteration 2000 is 1.2994575430802513e-05.
Converged in 2192 iterations.
Numba execution time = 52.71884536743164
jax_time_without_compile / numba_time_without_compile
0.036499129264701724
The JAX code is significantly faster, as expected.
This difference will increase when more features (and state variables) are added to the model.