11. Optimal Savings I: Value Function Iteration#
GPU
This lecture was built using a machine with JAX installed and access to a GPU.
To run this lecture on Google Colab, click on the “play” icon top right, select Colab, and set the runtime environment to include a GPU.
To run this lecture on your own machine, you need to install Google JAX.
In addition to JAX and Anaconda, this lecture will need the following libraries:
!pip install quantecon
Show code cell output
Requirement already satisfied: quantecon in /opt/conda/envs/quantecon/lib/python3.12/site-packages (0.7.2)
Requirement already satisfied: numba>=0.49.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (0.60.0)
Requirement already satisfied: numpy>=1.17.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.26.4)
Requirement already satisfied: requests in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (2.32.3)
Requirement already satisfied: scipy>=1.5.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.13.1)
Requirement already satisfied: sympy in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.13.2)
Requirement already satisfied: llvmlite<0.44,>=0.43.0dev0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from numba>=0.49.0->quantecon) (0.43.0)
Requirement already satisfied: charset-normalizer<4,>=2 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (3.3.2)
Requirement already satisfied: idna<4,>=2.5 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (3.7)
Requirement already satisfied: urllib3<3,>=1.21.1 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (2.2.3)
Requirement already satisfied: certifi>=2017.4.17 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (2024.8.30)
Requirement already satisfied: mpmath<1.4,>=1.1.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from sympy->quantecon) (1.3.0)
WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager, possibly rendering your system unusable.It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv. Use the --root-user-action option if you know what you are doing and want to suppress this warning.
We will use the following imports:
import quantecon as qe
import numpy as np
import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
from collections import namedtuple
from time import time
Let’s check the GPU we are running
!nvidia-smi
Wed Nov 20 00:35:34 2024
+---------------------------------------------------------------------------------------+
| NVIDIA-SMI 535.54.03 Driver Version: 535.54.03 CUDA Version: 12.6 |
|-----------------------------------------+----------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+======================+======================|
| 0 Tesla T4 On | 00000001:00:00.0 Off | 0 |
| N/A 48C P8 12W / 70W | 2MiB / 15360MiB | 0% Default |
| | | N/A |
+-----------------------------------------+----------------------+----------------------+
+---------------------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=======================================================================================|
| No running processes found |
+---------------------------------------------------------------------------------------+
We’ll use 64 bit floats to gain extra precision.
jax.config.update("jax_enable_x64", True)
11.1. Overview#
We consider an optimal savings problem with CRRA utility and budget constraint
where
\(C_t\) is consumption and \(C_t \geq 0\),
\(W_t\) is wealth and \(W_t \geq 0\),
\(R > 0\) is a gross rate of return, and
\((Y_t)\) is labor income.
We assume below that labor income is a discretized AR(1) process.
The Bellman equation is
where
In the code we use the function
the encapsulate the right hand side of the Bellman equation.
11.2. Starting with NumPy#
Let’s start with a standard NumPy version running on the CPU.
Starting with this traditional approach will allow us to record the speed gain associated with switching to JAX.
(NumPy operations are similar to MATLAB operations, so this also serves as a rough comparison with MATLAB.)
11.2.1. Functions and operators#
The following function contains default parameters and returns tuples that contain the key computational components of the model.
def create_consumption_model(R=1.01, # Gross interest rate
β=0.98, # Discount factor
γ=2, # CRRA parameter
w_min=0.01, # Min wealth
w_max=5.0, # Max wealth
w_size=150, # Grid side
ρ=0.9, ν=0.1, y_size=100): # Income parameters
"""
A function that takes in parameters and returns parameters and grids
for the optimal savings problem.
"""
# Build grids and transition probabilities
w_grid = np.linspace(w_min, w_max, w_size)
mc = qe.tauchen(n=y_size, rho=ρ, sigma=ν)
y_grid, Q = np.exp(mc.state_values), mc.P
# Pack and return
params = β, R, γ
sizes = w_size, y_size
arrays = w_grid, y_grid, Q
return params, sizes, arrays
(The function returns sizes of arrays because we use them later to help compile functions in JAX.)
To produce efficient NumPy code, we will use a vectorized approach.
The first step is to create the right hand side of the Bellman equation as a multi-dimensional array with dimensions over all states and controls.
def B(v, params, sizes, arrays):
"""
A vectorized version of the right-hand side of the Bellman equation
(before maximization), which is a 3D array representing
B(w, y, w′) = u(Rw + y - w′) + β Σ_y′ v(w′, y′) Q(y, y′)
for all (w, y, w′).
"""
# Unpack
β, R, γ = params
w_size, y_size = sizes
w_grid, y_grid, Q = arrays
# Compute current rewards r(w, y, wp) as array r[i, j, ip]
w = np.reshape(w_grid, (w_size, 1, 1)) # w[i] -> w[i, j, ip]
y = np.reshape(y_grid, (1, y_size, 1)) # z[j] -> z[i, j, ip]
wp = np.reshape(w_grid, (1, 1, w_size)) # wp[ip] -> wp[i, j, ip]
c = R * w + y - wp
# Calculate continuation rewards at all combinations of (w, y, wp)
v = np.reshape(v, (1, 1, w_size, y_size)) # v[ip, jp] -> v[i, j, ip, jp]
Q = np.reshape(Q, (1, y_size, 1, y_size)) # Q[j, jp] -> Q[i, j, ip, jp]
EV = np.sum(v * Q, axis=3) # sum over last index jp
# Compute the right-hand side of the Bellman equation
return np.where(c > 0, c**(1-γ)/(1-γ) + β * EV, -np.inf)
Here are two functions we need for value function iteration.
The first is the Bellman operator.
The second computes a \(v\)-greedy policy given \(v\) (i.e., the policy that maximizes the right-hand side of the Bellman equation.)
def T(v, params, sizes, arrays):
"The Bellman operator."
return np.max(B(v, params, sizes, arrays), axis=2)
def get_greedy(v, params, sizes, arrays):
"Computes a v-greedy policy, returned as a set of indices."
return np.argmax(B(v, params, sizes, arrays), axis=2)
11.2.2. Value function iteration#
Here’s a routine that performs value function iteration.
def value_function_iteration(model, max_iter=10_000, tol=1e-5):
params, sizes, arrays = model
v = np.zeros(sizes)
i, error = 0, tol + 1
while error > tol and i < max_iter:
v_new = T(v, params, sizes, arrays)
error = np.max(np.abs(v_new - v))
i += 1
v = v_new
return v, get_greedy(v, params, sizes, arrays)
Now we create an instance, unpack it, and test how long it takes to solve the model.
model = create_consumption_model()
# Unpack
params, sizes, arrays = model
β, R, γ = params
w_size, y_size = sizes
w_grid, y_grid, Q = arrays
print("Starting VFI.")
start = time()
v_star, σ_star = value_function_iteration(model)
numpy_with_compile = time() - start
print(f"VFI completed in {numpy_with_compile} seconds.")
Starting VFI.
VFI completed in 10.923219442367554 seconds.
Let’s run it again to eliminate compile time.
start = time()
v_star, σ_star = value_function_iteration(model)
numpy_without_compile = time() - start
print(f"VFI completed in {numpy_without_compile} seconds.")
VFI completed in 11.242656946182251 seconds.
Here’s a plot of the policy function.
fig, ax = plt.subplots()
ax.plot(w_grid, w_grid, "k--", label="45")
ax.plot(w_grid, w_grid[σ_star[:, 1]], label="$\\sigma^*(\cdot, y_1)$")
ax.plot(w_grid, w_grid[σ_star[:, -1]], label="$\\sigma^*(\cdot, y_N)$")
ax.legend()
plt.show()
<>:3: SyntaxWarning: invalid escape sequence '\c'
<>:4: SyntaxWarning: invalid escape sequence '\c'
<>:3: SyntaxWarning: invalid escape sequence '\c'
<>:4: SyntaxWarning: invalid escape sequence '\c'
/tmp/ipykernel_2377/2705187179.py:3: SyntaxWarning: invalid escape sequence '\c'
ax.plot(w_grid, w_grid[σ_star[:, 1]], label="$\\sigma^*(\cdot, y_1)$")
/tmp/ipykernel_2377/2705187179.py:4: SyntaxWarning: invalid escape sequence '\c'
ax.plot(w_grid, w_grid[σ_star[:, -1]], label="$\\sigma^*(\cdot, y_N)$")
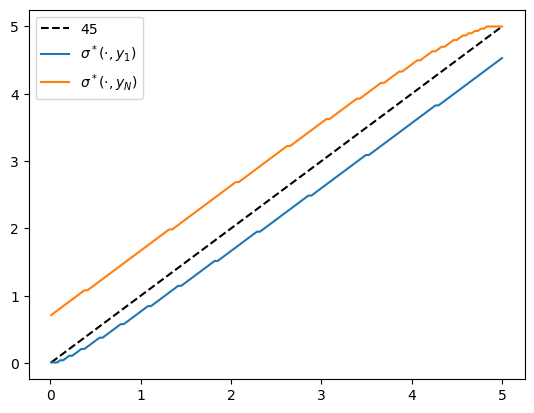
Fig. 11.1 Policy function#
11.3. Switching to JAX#
To switch over to JAX, we change np to jnp throughout and add some
jax.jit requests.
11.3.1. Functions and operators#
We redefine create_consumption_model to produce JAX arrays.
def create_consumption_model(R=1.01, # Gross interest rate
β=0.98, # Discount factor
γ=2, # CRRA parameter
w_min=0.01, # Min wealth
w_max=5.0, # Max wealth
w_size=150, # Grid side
ρ=0.9, ν=0.1, y_size=100): # Income parameters
"""
A function that takes in parameters and returns parameters and grids
for the optimal savings problem.
"""
w_grid = jnp.linspace(w_min, w_max, w_size)
mc = qe.tauchen(n=y_size, rho=ρ, sigma=ν)
y_grid, Q = jnp.exp(mc.state_values), jax.device_put(mc.P)
sizes = w_size, y_size
return (β, R, γ), sizes, (w_grid, y_grid, Q)
The right hand side of the Bellman equation is the same as the NumPy version
after switching np to jnp.
def B(v, params, sizes, arrays):
"""
A vectorized version of the right-hand side of the Bellman equation
(before maximization), which is a 3D array representing
B(w, y, w′) = u(Rw + y - w′) + β Σ_y′ v(w′, y′) Q(y, y′)
for all (w, y, w′).
"""
# Unpack
β, R, γ = params
w_size, y_size = sizes
w_grid, y_grid, Q = arrays
# Compute current rewards r(w, y, wp) as array r[i, j, ip]
w = jnp.reshape(w_grid, (w_size, 1, 1)) # w[i] -> w[i, j, ip]
y = jnp.reshape(y_grid, (1, y_size, 1)) # z[j] -> z[i, j, ip]
wp = jnp.reshape(w_grid, (1, 1, w_size)) # wp[ip] -> wp[i, j, ip]
c = R * w + y - wp
# Calculate continuation rewards at all combinations of (w, y, wp)
v = jnp.reshape(v, (1, 1, w_size, y_size)) # v[ip, jp] -> v[i, j, ip, jp]
Q = jnp.reshape(Q, (1, y_size, 1, y_size)) # Q[j, jp] -> Q[i, j, ip, jp]
EV = jnp.sum(v * Q, axis=3) # sum over last index jp
# Compute the right-hand side of the Bellman equation
return jnp.where(c > 0, c**(1-γ)/(1-γ) + β * EV, -jnp.inf)
Some readers might be concerned that we are creating high dimensional arrays, leading to inefficiency.
Could they be avoided by more careful vectorization?
In fact this is not necessary: this function will be JIT-compiled by JAX, and the JIT compiler will optimize compiled code to minimize memory use.
B = jax.jit(B, static_argnums=(2,))
In the call above, we indicate to the compiler that sizes is static, so the
compiler can parallelize optimally while taking array sizes as fixed.
The Bellman operator \(T\) can be implemented by
def T(v, params, sizes, arrays):
"The Bellman operator."
return jnp.max(B(v, params, sizes, arrays), axis=2)
T = jax.jit(T, static_argnums=(2,))
The next function computes a \(v\)-greedy policy given \(v\) (i.e., the policy that maximizes the right-hand side of the Bellman equation.)
def get_greedy(v, params, sizes, arrays):
"Computes a v-greedy policy, returned as a set of indices."
return jnp.argmax(B(v, params, sizes, arrays), axis=2)
get_greedy = jax.jit(get_greedy, static_argnums=(2,))
11.3.2. Successive approximation#
Now we define a solver that implements VFI.
We could use the one we built for NumPy above, after changing np to jnp.
Alternatively, we can push a bit harder and write a compiled version using
jax.lax.while_loop.
This will give us just a bit more speed.
The first step is to write a compiled successive approximation routine that
performs fixed point iteration on some given function T.
def successive_approx_jax(T, # Operator (callable)
x_0, # Initial condition
tolerance=1e-6, # Error tolerance
max_iter=10_000): # Max iteration bound
def body_fun(k_x_err):
k, x, error = k_x_err
x_new = T(x)
error = jnp.max(jnp.abs(x_new - x))
return k + 1, x_new, error
def cond_fun(k_x_err):
k, x, error = k_x_err
return jnp.logical_and(error > tolerance, k < max_iter)
k, x, error = jax.lax.while_loop(cond_fun, body_fun,
(1, x_0, tolerance + 1))
return x
successive_approx_jax = \
jax.jit(successive_approx_jax, static_argnums=(0,))
Our value function iteration routine calls successive_approx_jax while passing
in the Bellman operator.
def value_function_iteration(model, tol=1e-5):
params, sizes, arrays = model
vz = jnp.zeros(sizes)
_T = lambda v: T(v, params, sizes, arrays)
v_star = successive_approx_jax(_T, vz, tolerance=tol)
return v_star, get_greedy(v_star, params, sizes, arrays)
11.3.3. Timing#
Let’s create an instance and unpack it.
model = create_consumption_model()
# Unpack
params, sizes, arrays = model
β, R, γ = params
w_size, y_size = sizes
w_grid, y_grid, Q = arrays
Let’s see how long it takes to solve this model.
print("Starting VFI using vectorization.")
start = time()
v_star_jax, σ_star_jax = value_function_iteration(model)
jax_with_compile = time() - start
print(f"VFI completed in {jax_with_compile} seconds.")
Starting VFI using vectorization.
VFI completed in 0.8332741260528564 seconds.
Let’s run it again to eliminate compile time.
start = time()
v_star_jax, σ_star_jax = value_function_iteration(model)
jax_without_compile = time() - start
print(f"VFI completed in {jax_without_compile} seconds.")
VFI completed in 0.34981536865234375 seconds.
The relative speed gain is
print(f"Relative speed gain = {numpy_without_compile / jax_without_compile}")
Relative speed gain = 32.1388308052169
This is an impressive speed up and in fact we can do better still by switching to alternative algorithms that are better suited to parallelization.
These algorithms are discussed in a separate lecture.
11.4. Switching to vmap#
Before we discuss alternative algorithms, let’s take another look at value function iteration.
For this simple optimal savings problem, direct vectorization is relatively easy.
In particular, it’s straightforward to express the right hand side of the Bellman equation as an array that stores evaluations of the function at every state and control.
For more complex models direct vectorization can be much harder.
For this reason, it helps to have another approach to fast JAX implementations up our sleeves.
Here’s a version that
writes the right hand side of the Bellman operator as a function of individual states and controls, and
applies
jax.vmapon the outside to achieve a parallelized solution.
First let’s rewrite B
def B(v, params, arrays, i, j, ip):
"""
The right-hand side of the Bellman equation before maximization, which takes
the form
B(w, y, w′) = u(Rw + y - w′) + β Σ_y′ v(w′, y′) Q(y, y′)
The indices are (i, j, ip) -> (w, y, w′).
"""
β, R, γ = params
w_grid, y_grid, Q = arrays
w, y, wp = w_grid[i], y_grid[j], w_grid[ip]
c = R * w + y - wp
EV = jnp.sum(v[ip, :] * Q[j, :])
return jnp.where(c > 0, c**(1-γ)/(1-γ) + β * EV, -jnp.inf)
Now we successively apply vmap to simulate nested loops.
B_1 = jax.vmap(B, in_axes=(None, None, None, None, None, 0))
B_2 = jax.vmap(B_1, in_axes=(None, None, None, None, 0, None))
B_vmap = jax.vmap(B_2, in_axes=(None, None, None, 0, None, None))
Here’s the Bellman operator and the get_greedy functions for the vmap case.
def T_vmap(v, params, sizes, arrays):
"The Bellman operator."
w_size, y_size = sizes
w_indices, y_indices = jnp.arange(w_size), jnp.arange(y_size)
B_values = B_vmap(v, params, arrays, w_indices, y_indices, w_indices)
return jnp.max(B_values, axis=-1)
T_vmap = jax.jit(T_vmap, static_argnums=(2,))
def get_greedy_vmap(v, params, sizes, arrays):
"Computes a v-greedy policy, returned as a set of indices."
w_size, y_size = sizes
w_indices, y_indices = jnp.arange(w_size), jnp.arange(y_size)
B_values = B_vmap(v, params, arrays, w_indices, y_indices, w_indices)
return jnp.argmax(B_values, axis=-1)
get_greedy_vmap = jax.jit(get_greedy_vmap, static_argnums=(2,))
Here’s the iteration routine.
def value_iteration_vmap(model, tol=1e-5):
params, sizes, arrays = model
vz = jnp.zeros(sizes)
_T = lambda v: T_vmap(v, params, sizes, arrays)
v_star = successive_approx_jax(_T, vz, tolerance=tol)
return v_star, get_greedy(v_star, params, sizes, arrays)
Let’s see how long it takes to solve the model using the vmap method.
print("Starting VFI using vmap.")
start = time()
v_star_vmap, σ_star_vmap = value_iteration_vmap(model)
jax_vmap_with_compile = time() - start
print(f"VFI completed in {jax_vmap_with_compile} seconds.")
Starting VFI using vmap.
VFI completed in 0.467862606048584 seconds.
Let’s run it again to get rid of compile time.
start = time()
v_star_vmap, σ_star_vmap = value_iteration_vmap(model)
jax_vmap_without_compile = time() - start
print(f"VFI completed in {jax_vmap_without_compile} seconds.")
VFI completed in 0.3621225357055664 seconds.
We need to make sure that we got the same result.
print(jnp.allclose(v_star_vmap, v_star_jax))
print(jnp.allclose(σ_star_vmap, σ_star_jax))
True
True
Here’s the speed gain associated with switching from the NumPy version to JAX with vmap:
print(f"Relative speed = {numpy_without_compile/jax_vmap_without_compile}")
Relative speed = 31.04655423964942
And here’s the comparison with the first JAX implementation (which used direct vectorization).
print(f"Relative speed = {jax_without_compile / jax_vmap_without_compile}")
Relative speed = 0.9660138051633734
The execution times for the two JAX versions are relatively similar.
However, as emphasized above, having a second method up our sleeves (i.e, the
vmap approach) will be helpful when confronting dynamic programs with more
sophisticated Bellman equations.