21. Maximum Likelihood Estimation#

GPU

This lecture was built using a machine with JAX installed and access to a GPU.

To run this lecture on Google Colab, click on the “play” icon top right, select Colab, and set the runtime environment to include a GPU.

To run this lecture on your own machine, you need to install Google JAX.

21.1. Overview#

This lecture is the extended JAX implementation of this section of this lecture.

Please refer that lecture for all background and notation.

Here we will exploit the automatic differentiation capabilities of JAX rather than calculating derivatives by hand.

We’ll require the following imports:

import matplotlib.pyplot as plt
from collections import namedtuple
import jax.numpy as jnp
import jax
from statsmodels.api import Poisson

Let’s check the GPU we are running

!nvidia-smi

Wed Nov 20 00:32:48 2024       
+---------------------------------------------------------------------------------------+
| NVIDIA-SMI 535.54.03              Driver Version: 535.54.03    CUDA Version: 12.6     |
|-----------------------------------------+----------------------+----------------------+
| GPU  Name                 Persistence-M | Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp   Perf          Pwr:Usage/Cap |         Memory-Usage | GPU-Util  Compute M. |
|                                         |                      |               MIG M. |
|=========================================+======================+======================|
|   0  Tesla T4                       On  | 00000001:00:00.0 Off |                    0 |
| N/A   44C    P0              28W /  70W |      2MiB / 15360MiB |      0%      Default |
|                                         |                      |                  N/A |
+-----------------------------------------+----------------------+----------------------+
                                                                                         
+---------------------------------------------------------------------------------------+
| Processes:                                                                            |
|  GPU   GI   CI        PID   Type   Process name                            GPU Memory |
|        ID   ID                                                             Usage      |
|=======================================================================================|
|  No running processes found                                                           |
+---------------------------------------------------------------------------------------+

We will use 64 bit floats with JAX in order to increase the precision.

jax.config.update("jax_enable_x64", True)

21.2. MLE with numerical methods (JAX)#

Many distributions do not have nice, analytical solutions and therefore require numerical methods to solve for parameter estimates.

One such numerical method is the Newton-Raphson algorithm.

Let’s start with a simple example to illustrate the algorithm.

21.2.1. A toy model#

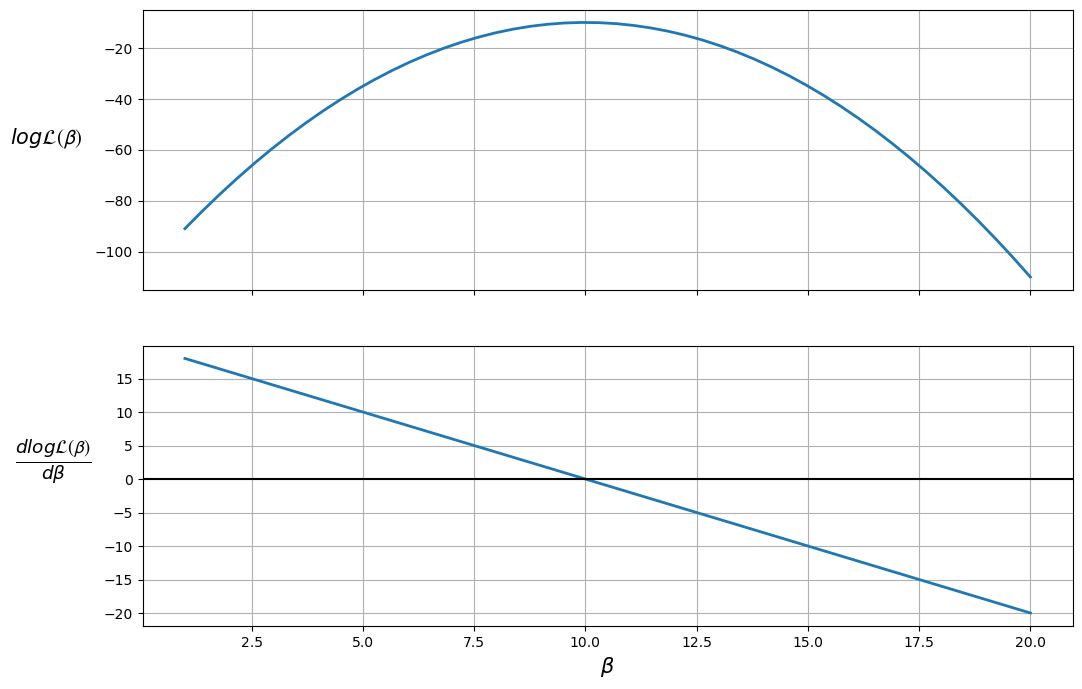
Our goal is to find the maximum likelihood estimate \(\hat{\boldsymbol{\beta}}\).

At \(\hat{\boldsymbol{\beta}}\), the first derivative of the log-likelihood function will be equal to 0.

Let’s illustrate this by supposing

\[ \log \mathcal{L(\beta)} = - (\beta - 10) ^2 - 10 \]

Define the function logL.

@jax.jit
def logL(β):
    return -(β - 10) ** 2 - 10

To find the value of \(\frac{d \log \mathcal{L(\boldsymbol{\beta})}}{d \boldsymbol{\beta}}\), we can use jax.grad which auto-differentiates the given function.

We further use jax.vmap which vectorizes the given function i.e. the function acting upon scalar inputs can now be used with vector inputs.

dlogL = jax.vmap(jax.grad(logL))

β = jnp.linspace(1, 20)

fig, (ax1, ax2) = plt.subplots(2, sharex=True, figsize=(12, 8))

ax1.plot(β, logL(β), lw=2)
ax2.plot(β, dlogL(β), lw=2)

ax1.set_ylabel(r'$log \mathcal{L(\beta)}$',
               rotation=0,
               labelpad=35,
               fontsize=15)
ax2.set_ylabel(r'$\frac{dlog \mathcal{L(\beta)}}{d \beta}$ ',
               rotation=0,
               labelpad=35,
               fontsize=19)

ax2.set_xlabel(r'$\beta$', fontsize=15)
ax1.grid(), ax2.grid()
plt.axhline(c='black')
plt.show()
_images/99543c3421430efd2323bf914ce4d5e23c0f4141b1e1408271ad3f14122095db.png

The plot shows that the maximum likelihood value (the top plot) occurs when \(\frac{d \log \mathcal{L(\boldsymbol{\beta})}}{d \boldsymbol{\beta}} = 0\) (the bottom plot).

Therefore, the likelihood is maximized when \(\beta = 10\).

We can also ensure that this value is a maximum (as opposed to a minimum) by checking that the second derivative (slope of the bottom plot) is negative.

The Newton-Raphson algorithm finds a point where the first derivative is 0.

To use the algorithm, we take an initial guess at the maximum value, \(\beta_0\) (the OLS parameter estimates might be a reasonable guess).

Then we use the updating rule involving gradient information to iterate the algorithm until the error is sufficiently small or the algorithm reaches the maximum number of iterations.

Please refer to this section for the detailed algorithm.

21.2.2. A Poisson model#

Let’s have a go at implementing the Newton-Raphson algorithm to calculate the maximum likelihood estimations of a Poisson regression.

The Poisson regression has a joint pmf:

\[ f(y_1, y_2, \ldots, y_n \mid \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n; \boldsymbol{\beta}) = \prod_{i=1}^{n} \frac{\mu_i^{y_i}}{y_i!} e^{-\mu_i}\]
\[ \text{where}\ \mu_i = \exp(\mathbf{x}_i' \boldsymbol{\beta}) = \exp(\beta_0 + \beta_1 x_{i1} + \ldots + \beta_k x_{ik}) \]

We create a namedtuple to store the observed values

RegressionModel = namedtuple('RegressionModel', ['X', 'y'])

def create_regression_model(X, y):
    n, k = X.shape
    # Reshape y as a n_by_1 column vector
    y = y.reshape(n, 1)
    X, y = jax.device_put((X, y))
    return RegressionModel(X=X, y=y)

The log likelihood function of the Poisson regression is

\[ \underset{\beta}{\max} \Big( \sum_{i=1}^{n} y_i \log{\mu_i} - \sum_{i=1}^{n} \mu_i - \sum_{i=1}^{n} \log y! \Big) \]

The full derivation can be found here.

The log likelihood function involves factorial, but JAX doesn’t have a readily available implementation to compute factorial directly.

In order to compute the factorial efficiently such that we can JIT it, we use

\[ n! = e^{\log(\Gamma(n+1))} \]

since jax.lax.lgamma and jax.lax.exp are available.

The following function jax_factorial computes the factorial using this idea.

Let’s define this function in Python

@jax.jit
def _factorial(n):
    return jax.lax.exp(jax.lax.lgamma(n + 1.0)).astype(int)

jax_factorial = jax.vmap(_factorial)

Now we can define the log likelihood function in Python

@jax.jit
def poisson_logL(β, model):
    y = model.y
    μ = jnp.exp(model.X @ β)
    return jnp.sum(model.y * jnp.log(μ) - μ - jnp.log(jax_factorial(y)))

To find the gradient of the poisson_logL, we again use jax.grad.

According to the documentation,

  • jax.jacfwd uses forward-mode automatic differentiation, which is more efficient for “tall” Jacobian matrices, while

  • jax.jacrev uses reverse-mode, which is more efficient for “wide” Jacobian matrices.

(The documentation also states that when matrices that are near-square, jax.jacfwd probably has an edge over jax.jacrev.)

Therefore, to find the Hessian, we can directly use jax.jacfwd.

G_poisson_logL = jax.grad(poisson_logL)
H_poisson_logL = jax.jacfwd(G_poisson_logL)

Our function newton_raphson will take a RegressionModel object that has an initial guess of the parameter vector \(\boldsymbol{\beta}_0\).

The algorithm will update the parameter vector according to the updating rule, and recalculate the gradient and Hessian matrices at the new parameter estimates.

def newton_raphson(model, β, tol=1e-3, max_iter=100, display=True):

    i = 0
    error = 100  # Initial error value

    # Print header of output
    if display:
        header = f'{"Iteration_k":<13}{"Log-likelihood":<16}{"θ":<60}'
        print(header)
        print("-" * len(header))

    # While loop runs while any value in error is greater
    # than the tolerance until max iterations are reached
    while jnp.any(error > tol) and i < max_iter:
        H, G = jnp.squeeze(H_poisson_logL(β, model)), G_poisson_logL(β, model)
        β_new = β - (jnp.dot(jnp.linalg.inv(H), G))
        error = jnp.abs(β_new - β)
        β = β_new

        if display:
            β_list = [f'{t:.3}' for t in list(β.flatten())]
            update = f'{i:<13}{poisson_logL(β, model):<16.8}{β_list}'
            print(update)

        i += 1

    print(f'Number of iterations: {i}')
    print(f'β_hat = {β.flatten()}')

    return β

Let’s try out our algorithm with a small dataset of 5 observations and 3 variables in \(\mathbf{X}\).

X = jnp.array([[1, 2, 5],
               [1, 1, 3],
               [1, 4, 2],
               [1, 5, 2],
               [1, 3, 1]])

y = jnp.array([1, 0, 1, 1, 0])

# Take a guess at initial βs
init_β = jnp.array([0.1, 0.1, 0.1]).reshape(X.shape[1], 1)

# Create an object with Poisson model values
poi = create_regression_model(X, y)

# Use newton_raphson to find the MLE
β_hat = newton_raphson(poi, init_β, display=True)

Iteration_k  Log-likelihood  θ                                                           
-----------------------------------------------------------------------------------------

0            -4.3447622      ['-1.49', '0.265', '0.244']
1            -3.5742413      ['-3.38', '0.528', '0.474']
2            -3.3999526      ['-5.06', '0.782', '0.702']
3            -3.3788646      ['-5.92', '0.909', '0.82']
4            -3.3783559      ['-6.07', '0.933', '0.843']
5            -3.3783555      ['-6.08', '0.933', '0.843']
6            -3.3783555      ['-6.08', '0.933', '0.843']
Number of iterations: 7
β_hat = [-6.07848573  0.9334028   0.84329677]

As this was a simple model with few observations, the algorithm achieved convergence in only 7 iterations.

The gradient vector should be close to 0 at \(\hat{\boldsymbol{\beta}}\)

G_poisson_logL(β_hat, poi)

Array([[-2.53297383e-13],
       [-6.40432152e-13],
       [-4.93882713e-13]], dtype=float64)

21.3. MLE with statsmodels#

We’ll use the Poisson regression model in statsmodels to verify the results obtained using JAX.

statsmodels uses the same algorithm as above to find the maximum likelihood estimates.

Now, as statsmodels accepts only NumPy arrays, we can use the __array__ method of JAX arrays to convert it to NumPy arrays.

X_numpy = X.__array__()
y_numpy = y.__array__()

stats_poisson = Poisson(y_numpy, X_numpy).fit()
print(stats_poisson.summary())

Optimization terminated successfully.
         Current function value: 0.675671
         Iterations 7
                          Poisson Regression Results                          
==============================================================================
Dep. Variable:                      y   No. Observations:                    5
Model:                        Poisson   Df Residuals:                        2
Method:                           MLE   Df Model:                            2
Date:                Wed, 20 Nov 2024   Pseudo R-squ.:                  0.2546
Time:                        00:32:51   Log-Likelihood:                -3.3784
converged:                       True   LL-Null:                       -4.5325
Covariance Type:            nonrobust   LLR p-value:                    0.3153
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const         -6.0785      5.279     -1.151      0.250     -16.425       4.268
x1             0.9334      0.829      1.126      0.260      -0.691       2.558
x2             0.8433      0.798      1.057      0.291      -0.720       2.407
==============================================================================

The benefit of writing our own procedure, relative to statsmodels is that

  • we can exploit the power of the GPU and

  • we learn the underlying methodology, which can be extended to complex situations where no existing routines are available.

Exercise 21.1

We define a quadratic model for a single explanatory variable by

\[ \log(\lambda_t) = \beta_0 + \beta_1 x_t + \beta_2 x_{t}^2 \]

We calculate the mean on the original scale instead of the log scale by exponentiating both sides of the above equation, which gives

(21.1)#\[ \lambda_t = \exp(\beta_0 + \beta_1 x_t + \beta_2 x_{t}^2)\]

Simulate the values of \(x_t\) by sampling from a normal distribution and \(\lambda_t\) by using (21.1) and the following constants:

\[ \beta_0 = -2.5, \quad \beta_1 = 0.25, \quad \beta_2 = 0.5 \]

Try to obtain the approximate values of \(\beta_0,\beta_1,\beta_2\), by simulating a Poisson Regression Model such that

\[ y_t \sim {\rm Poisson}(\lambda_t) \quad \text{for all } t. \]

Using our newton_raphson function on the data set \(X = [1, x_t, x_t^{2}]\) and \(y\), obtain the maximum likelihood estimates of \(\beta_0,\beta_1,\beta_2\).

With a sufficient large sample size, you should approximately recover the true values of of these parameters.