20. Bianchi Overborrowing Model#

GPU

This lecture was built using a machine with JAX installed and access to a GPU.

To run this lecture on Google Colab, click on the “play” icon top right, select Colab, and set the runtime environment to include a GPU.

To run this lecture on your own machine, you need to install Google JAX.

This lecture provides a JAX implementation of “Overborrowing and Systemic Externalities” [Bianchi, 2011] by Javier Bianchi.

In addition to what’s in Anaconda, this lecture will need the following libraries:

!pip install quantecon
Hide code cell output 
Requirement already satisfied: quantecon in /opt/conda/envs/quantecon/lib/python3.12/site-packages (0.7.2)
Requirement already satisfied: numba>=0.49.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (0.60.0)
Requirement already satisfied: numpy>=1.17.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.26.4)
Requirement already satisfied: requests in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (2.32.3)
Requirement already satisfied: scipy>=1.5.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.13.1)
Requirement already satisfied: sympy in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.13.2)
Requirement already satisfied: llvmlite<0.44,>=0.43.0dev0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from numba>=0.49.0->quantecon) (0.43.0)
Requirement already satisfied: charset-normalizer<4,>=2 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (3.3.2)
Requirement already satisfied: idna<4,>=2.5 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (3.7)
Requirement already satisfied: urllib3<3,>=1.21.1 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (2.2.3)
Requirement already satisfied: certifi>=2017.4.17 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (2024.8.30)
Requirement already satisfied: mpmath<1.4,>=1.1.0 in /opt/conda/envs/quantecon/lib/python3.12/site-packages (from sympy->quantecon) (1.3.0)

WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager, possibly rendering your system unusable.It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv. Use the --root-user-action option if you know what you are doing and want to suppress this warning.

We use the following imports.

import time
import jax
import numba
import jax.numpy as jnp
import matplotlib.pyplot as plt
import numpy as np
import quantecon as qe
import scipy as sp
import matplotlib.pyplot as plt
from collections import namedtuple

20.1. Markov dynamics#

Before studying Bianchi (2011), we develop some functions for working with the bivariate VAR process

\[ \ln y' = A \ln y + u' \]

where

  • prime indicates next period value

  • \(y = (y_t, y_n) = \) output of (tradables, nontradables)

  • \(u' \sim N(0, \Omega)\) and \(\Omega\) is positive definite

  • the log function is applied pointwise

We use the following estimated values, reported on p. 12 of Yamada (2023).

A = [[0.2425,   0.3297],
     [-0.1984,  0.7576]]

Ω = [[0.0052, 0.002],
     [0.002,  0.0059]]

A, Ω = np.array(A), np.array(Ω)

We’ll store the data in \(\Omega\) using its square root:

C = sp.linalg.sqrtm(Ω)

20.1.1. Simulating the VAR#

Here’s code for generating the original VAR process, which can be used for testing.

@numba.jit
def generate_var_process(A=A, C=C, ts_length=1_000_000):
    """
    Generate the original VAR process.

    """
    y_series = np.empty((ts_length, 2))
    y_series[0, :] = np.zeros(2)
    for t in range(ts_length-1):
        y_series[t+1, :] = A @ y_series[t, :] + C @ np.random.randn(2)
    y_t_series = np.exp(y_series[:, 0])
    y_n_series = np.exp(y_series[:, 1])
    return y_t_series, y_n_series

20.1.2. Discretizing the VAR#

Here’s a function to convert the VAR process to a Markov chain evolving on a rectilinear grid of points in \(\mathbb R^2\).

The function returns arrays y_t, y_n and Q

  • Q[i, j, i', j'] is the probability of moving from (y_t[i], y_n[j]) to (y_t[i'], y_n[j']).

Under the hood, this function uses the QuantEcon function discrete_var.

def discretize_income_var(A=A, C=C, n=4, seed=1234):
    """
    Discretize the VAR model, returning

        y_t, an n-grid of y_t values
        y_n, an n-grid of y_n values
        Q, a Markov operator

    The format is that Q is n x n x n x n, with

        Q[i, j, i', j'] = one step transition prob from 
        (y_t[i], y_n[j]) to (y_t[i'], y_n[j'])

    """ 
    rng = np.random.default_rng(seed)
    mc = qe.markov.discrete_var(A, C, (n, n),
                                sim_length=1_000_000,
                                std_devs=np.sqrt(3),
                                random_state=rng)
    y, Q = np.exp(mc.state_values), mc.P
    # The array y is currently an array listing all bivariate state pairs
    # (y_t, y_n), so that y[i] is the i-th such pair, while Q[l, m] 
    # is the probability of transitioning from state l to state m in one step. 
    # We switch the representation to the one described in the docstring.
    y_t = [y[n*i, 0] for i in range(n)]  
    y_n = y[0:4, 1]                      
    Q = np.reshape(Q, (n, n, n, n))
    return y_t, y_n, Q

Here’s code for sampling from the Markov chain.

def generate_discrete_var(A=A, C=C, n=4, seed=1234, 
                          ts_length=1_000_000,
                          indices=False):
    """
    Generate a time series from the discretized model, returning y_t_series and
    y_n_series.  If `indices=True`, then these series are returned as grid
    indices.
    """
    
    
    rng = np.random.default_rng(seed)
    mc = qe.markov.discrete_var(A, C, (n, n),
                                sim_length=1_000_000,
                                std_devs=np.sqrt(3),
                                random_state=rng)
    if indices:
        y_series = mc.simulate_indices(ts_length=ts_length)
        y_t_series, y_n_series = y_series % n, y_series // n
    else:
        y_series = np.exp(mc.simulate(ts_length=ts_length))
        y_t_series, y_n_series = y_series[:, 0], y_series[:, 1]
    return y_t_series, y_n_series

20.1.3. Testing the discretization#

Let’s check some statistics for both the original and the discretized processes, to see if they match up.

def corr(x, y):
    m_x, m_y = x.mean(), y.mean()
    s_xy = np.sqrt(np.sum((x - m_x)**2) * np.sum((y - m_y)**2))
    return np.sum((x - m_x) * (y - m_y)) / (s_xy)

def print_stats(y_t_series, y_n_series):
    print(f"Std dev of y_t is {y_t_series.std():.3}")
    print(f"Std dev of y_n is {y_n_series.std():.3}")
    print(f"corr(y_t, y_n) is {corr(y_t_series, y_n_series):.3}")
    print(f"auto_corr(y_t) is {corr(y_t_series[:-1], y_t_series[1:]):.3}")
    print(f"auto_corr(y_n) is {corr(y_n_series[:-1], y_n_series[1:]):.3}")
    print("\n")

print("Statistics for original process.\n")
print_stats(*generate_var_process())

Statistics for original process.

Std dev of y_t is 0.088
Std dev of y_n is 0.106
corr(y_t, y_n) is 0.541
auto_corr(y_t) is 0.455
auto_corr(y_n) is 0.669

print("Statistics for discretized process.\n")
print_stats(*generate_discrete_var())

Statistics for discretized process.

Std dev of y_t is 0.0876
Std dev of y_n is 0.105
corr(y_t, y_n) is 0.477
auto_corr(y_t) is 0.403
auto_corr(y_n) is 0.591

20.2. Description of the model#

The Bianchi (2011) model seeks to explain sudden stops in emerging market economies.

A representative household chooses how much to borrow on international markets and how much to consume.

The household is credit constrained, with the constraint depending on both current income and the real exchange rate.

Household “overborrow” (relative to a planner) because they do not internalize the effect of borrowing on the credit constraint.

This overborrowing leaves them vulnerable to bad income shocks.

In essence, the model works as follows

  1. During good times, households borrow more and consume more

  2. Increased consumption pushes up the price of nontradables and hence the real exchange rate

  3. A rising real exchange rate loosens the credit constraint and encourages more borrowing

  4. This leads to excessive borrowing relative to a planner.

This overborrowing leads to vulnerability vis-a-vis bad shocks.

  1. When a bad shock hits, borrowing is restricted.

  2. Consumption now falls, pushing down the real exchange rate.

  3. This fall in the exchange rate further tightens the borrowing constraint, amplifying the shock

20.2.1. Decentralized equilibrium#

The model contains a representative household that seeks to maximize an expected sum of discounted utility with

\[ u(c) = \frac{c^{1-\sigma}}{1-\sigma} \quad \text{where} \quad c = (\omega c_t^{-\eta} + (1-\omega) c_n^{-\eta})^{-1/\eta} \]

Here \(c_t\) (resp., \(c_n\)) is consumption of tradables (resp., nontradables).

The household maximizes subject to the budget constraint

\[ b' + c_t + p_n c_n = b (1+r) + y_t + p_n y_n \]

where

  • \(b\) is bond holdings (positive values denote assets!)

  • primes denote next period values

  • the interest rate \(r\) is exogenous

  • \(p_n\) is the price of nontradables, while the price of tradables is normalized to 1

  • \(y_t\) and \(y_n\) are current tradable and nontradable income

The process for \(y := (y_t, y_n)\) is first-order Markov.

The household also faces the credit constraint

\[ b' \geq - \kappa (y_t + p_n y_n) \]

Market clearing implies

\[ c_n = y_n \quad \text{and} \quad c_t = y_t + (1+r)b - b' \]

The household takes the aggregate timepath for bonds as given by

\[B' = H(B, y)\]

and solves

\[ v(b, B, y) = \max_{c, b'} \left\{ u(c) + \beta \, \mathbb{E}_y \, v(b', B', y') \right\} \]

subject to the budget and credit constraints.

Let the solution to the dynamic program be the policy \(b' = h(b, B, y) = \) savings decision in state \((b, B, y)\).

A decentralized equilibrium is a map \(H\) such that

\[ h(B, B, y) = H(B, y) \quad \text{for all } B, y \]

20.2.2. Notation#

Let

\[ w(c_t, y_n) = \frac{c^{1 - σ}}{1 - σ} \quad \text{where} \quad c = [ω c_t^{- η} + (1 - ω) y_n^{- η}]^{-1/η} \]

Using the market clearing conditions, we can write the household problem as

\[ v(b, B, y) = \max_{b'} \left\{ w((1 + r) b + y_t - b', y_n) + \beta \, \mathbb{E}_y \, v(b', H(B, y), y') \right\} \]

subject to

\[ - κ (p_n y_n + y_t) \leq b' \leq (1 + r) b + y_t \]

where \(p_n\) is given by

\[ p_n = \frac{1 - ω}{ ω} \left(\frac{C}{y_n} \right)^{η + 1} \quad \text{with} \quad C := (1 + r) B + y_t - H(B, y) \]

We will make use of the policy operator that maps \(h\) into

\[ (T_h v)(b, B, y) = \left\{ w((1 + r) b + y_t - h(b, B, y), y_n) + \beta \, \mathbb{E}_y \, v(h(b, B, y), H(B, y), y') \right\} \]

Our algorithm is

  1. initialize \(v\) and \(H\)

  2. get a greedy policy \(h\) given \(v\) and \(H\)

  3. update \(H\) via \(H = \alpha h + (1 - \alpha) H\)

  4. iterate \(m\) times with the policy operator \(T_h\) to get \(v = T^m_h v\)

  5. go to step 2

In other words, we use optimistic policy iteration, updating our guess of the aggregate law of motion every time we update the household policy function.

20.3. Overborrowing model in Python / JAX#

In what follows

  • y = (y_t, y_n) is the exogenous state process

Individual states and actions are

  • c = consumption of tradables (c rather than c_t)

  • b = household savings (bond holdings)

  • bp = household savings decision (next period bond holdings)

Aggregate quantities and prices are

  • p = price of nontradables (p rather than p_n)

  • B = aggregate savings (bond holdings)

  • C = aggregate consumption

  • H = current guess of update rule as an array of the form \(H(B, y)\)

Here’s code to create three tuples that store model data relevant for computation.

Model = namedtuple('Model',
    ('σ', 'η', 'β', 'ω', 'κ', 'r', 'b_grid', 'y_t_nodes', 'y_n_nodes', 'Q'))

def create_overborrowing_model(
        σ=2.0,               # CRRA utility parameter
        η=(1 / 0.83) - 1,    # Elasticity = 0.83, η = 0.2048
        β=0.91,              # Discount factor
        ω=0.31,              # Aggregation constant
        κ=0.3235,            # Constraint parameter
        r=0.04,              # Interest rate
        b_size=800,          # Bond grid size
        b_grid_min=-1.02,    # Bond grid min
        b_grid_max=-0.2      # Bond grid max (originally -0.6 to match fig)
    ):    
    """
    Creates an instance of the overborrowing model using 

        * default parameter values from Bianchi (2011)
        * Markov dynamics from Yamada (2023)

    The Markov kernel Q has the interpretation

        Q[i, j, ip, jp] = one step prob of moving 

            (y_t[i], y_n[j]) -> (y_t[ip], y_n[jp])

    """
    # Read in Markov data and shift to JAX arrays
    data = discretize_income_var()
    y_t_nodes, y_n_nodes, Q = [jnp.array(d) for d in data]
    # Set up grid for bond holdings
    b_grid = jnp.linspace(b_grid_min, b_grid_max, b_size)
    # Pack and return
    return Model(σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q)

Default parameter values are from Bianchi.

Notice that \(\beta\) is quite small (too small?), so value function iteration will be relatively quick.

Here’s flow utility.

@jax.jit
def w(model, c, y_n):
    """ 
    Current utility when c_t = c and c_n = y_n.

        a = [ω c^(- η) + (1 - ω) y_n^(- η)]^(-1/η)

        w(c, y_n) := a^(1 - σ) / (1 - σ)

    """
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    a = (ω * c**(-η) + (1 - ω) * y_n**(-η))**(-1/η)
    return a**(1 - σ) / (1 - σ)

We need code to generate an initial guess of \(H\).

@jax.jit
def generate_initial_H(model, at_constraint=False):
    """
    Compute an initial guess for H. Repeat the indices for b_grid over y_t and
    y_n axes.

    """
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    b_size, y_size = len(b_grid), len(y_t_nodes)
    b_indices = jnp.arange(b_size)
    O = jnp.ones((b_size, y_size, y_size), dtype=int)
    return  O * jnp.reshape(b_indices, (b_size, 1, 1))

We need to construct the Bellman operator for the household.

Our first function returns the (unmaximized) RHS of the Bellman equation.

@jax.jit
def BellmanRHS(model, v, H, i_b, i_B, i_y_t, i_y_n, i_bp):
    """
    Given current state (b, B, y_t, y_n) with indices (i_b, i_B, i_y_t, i_y_n),
    compute the unmaximized right hand side (RHS) of the Bellman equation as a
    function of the next period choice bp = b', with index i_bp.  
    """
    # Unpack
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    # Compute next period aggregate bonds given H
    i_Bp = H[i_B, i_y_t, i_y_n]
    # Evaluate states and actions at indices
    B, Bp, b, bp = b_grid[i_B], b_grid[i_Bp], b_grid[i_b], b_grid[i_bp]
    y_t = y_t_nodes[i_y_t]
    y_n = y_n_nodes[i_y_n]
    # Compute price of nontradables using aggregates
    C = (1 + r) * B + y_t - Bp
    p = ((1 - ω) / ω) * (C / y_n)**(η + 1)
    # Compute household flow utility
    c = (1 + r) * b + y_t - bp
    utility = w(model, c, y_n)
    # Compute expected value Σ_{y'} v(b', B', y') Q(y, y')
    EV = jnp.sum(v[i_bp, i_Bp, :, :] * Q[i_y_t, i_y_n, :, :])
    # Set up constraints 
    credit_constraint_holds = - κ * (p * y_n + y_t) <= bp
    budget_constraint_holds = bp <= (1 + r) * b + y_t
    constraints_hold = jnp.logical_and(credit_constraint_holds, 
                                     budget_constraint_holds)
    # Compute and return
    return jnp.where(constraints_hold, utility + β * EV, -jnp.inf)

Let’s now vectorize and jit-compile this map.

# Vectorize over the control bp and all the current states
BellmanRHS = jax.vmap(BellmanRHS,
    in_axes=(None, None, None, None, None, None, None, 0))
BellmanRHS = jax.vmap(BellmanRHS, 
    in_axes=(None, None, None, None, None, None, 0, None))
BellmanRHS = jax.vmap(BellmanRHS, 
    in_axes=(None, None, None, None, None, 0, None, None))
BellmanRHS = jax.vmap(BellmanRHS, 
    in_axes=(None, None, None, None, 0, None, None, None))
BellmanRHS = jax.vmap(BellmanRHS, 
    in_axes=(None, None, None, 0, None, None, None, None))

Here’s a function that computes a greedy policy (best response to \(v\)).

@jax.jit
def get_greedy(model, v, H):
    """
    Compute the greedy policy for the household, which maximizes the right hand
    side of the Bellman equation given v and H.  The greedy policy is recorded
    as an array giving the index i in b_grid such that b_grid[i] is the optimal
    choice, for every state.

    Return 

        * bp_policy as an array of shape (b_size, b_size, y_size, y_size).

    """
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    b_size, y_size = len(b_grid), len(y_t_nodes)
    b_indices, y_indices = jnp.arange(b_size), jnp.arange(y_size)
    val = BellmanRHS(model, v, H, 
                     b_indices, b_indices, y_indices, y_indices, b_indices)
    return jnp.argmax(val, axis=-1)

Here’s the policy operator

@jax.jit
def _T_h(model, h, v, H, i_b, i_B, i_y_t, i_y_n):
    """
    Evaluate the RHS of the policy operator associated with individual
    policy h and aggregate policy H.


    """
    # Unpack
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    # Compute next period states
    i_bp = h[i_b, i_B, i_y_t, i_y_n]
    i_Bp = H[i_B, i_y_t, i_y_n]
    # Convert indices into values
    B, Bp, b, bp = b_grid[i_B], b_grid[i_Bp], b_grid[i_b], b_grid[i_bp]
    y_t = y_t_nodes[i_y_t]
    y_n = y_n_nodes[i_y_n]
    # Compute household flow utility
    c = (1 + r) * b + y_t - bp
    utility = w(model, c, y_n)
    # Compute expected value Σ_{y'} v(b', B', y') Q(y, y')
    EV = jnp.sum(v[i_bp, i_Bp, :, :] * Q[i_y_t, i_y_n, :, :])
    val = utility + β * EV
    return val

# Vectorize over the control bp and all the current states
_T_h = jax.vmap(_T_h,
    in_axes=(None, None, None, None, None, None, None, 0))
_T_h = jax.vmap(_T_h, 
    in_axes=(None, None, None, None, None, None, 0, None))
_T_h = jax.vmap(_T_h, 
    in_axes=(None, None, None, None, None, 0, None, None))
_T_h = jax.vmap(_T_h, 
    in_axes=(None, None, None, None, 0, None, None, None))

@jax.jit
def T_h(model, h, v, H):
    """
    Vectorized version of the policy operator.

    """
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    b_size, y_size = len(b_grid), len(y_t_nodes)
    b_indices, y_indices = jnp.arange(b_size), jnp.arange(y_size)
    val = _T_h(model, h, v, H, 
                     b_indices, b_indices, y_indices, y_indices)
    return val

@jax.jit
def iterate_policy_operator(model, h, v, H, m):

    def update(i, v):
        v = T_h(model, h, v, H)
        return v
    v = jax.lax.fori_loop(0, m, update, v)
    return v

This is how we update our guess of \(H\), using the current policy \(b'\) and a damped fixed point iteration scheme.

@jax.jit
def update_H(model, H, h, α):
    """
    Update guess of the aggregate update rule.

    """
    # Set up
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    b_size, y_size = len(b_grid), len(y_t_nodes)
    b_indices = jnp.arange(b_size)
    # Switch policy arrays to values rather than indices
    H_vals = b_grid[H]
    bp_vals = b_grid[h]
    # Update guess
    new_H_vals = α * bp_vals[b_indices, b_indices, :, :] + (1 - α) * H_vals
    # Switch back to indices
    new_H = jnp.searchsorted(b_grid, new_H_vals)
    return new_H

Now we can write code to compute an equilibrium law of motion \(H\).

def compute_equilibrium(model, m=50,
                          α=0.5, tol=0.005, max_iter=500):
    """
    Compute the equilibrium law of motion.

    """
    H = generate_initial_H(model)
    v = jnp.ones((b_size, b_size, y_size, y_size))
    h = get_greedy(model, v, H)
    error = tol + 1
    i = 0
    while error > tol and i < max_iter:
        new_H = update_H(model, H, h, α)
        new_v = iterate_policy_operator(model, h, v, new_H, m)
        new_h = get_greedy(model, new_v, new_H)
        error = jnp.max(jnp.abs(b_grid[H] - b_grid[new_H]))
        print(f"Updated H at iteration {i} with error {error}.")
        H = new_H
        v = new_v
        h = new_h
        i += 1
    if i == max_iter:
        print("Warning: Equilibrium search iteration hit upper bound.")
    return H

20.4. Planner problem#

Now we switch to the planner problem.

The constrained planner solves

\[ V(b, B, y) = \max_{c, b'} \left\{ u(c) + \beta \mathbb{E}_y v(b', B', y') \right\} \]

subject to the market clearing conditions and the same constraint

\[ - \kappa (y_t + p_n y_n) \leq b' \leq (1+r) b + y_t \]

although the price of nontradable is now given by

\[ p_n = ((1 - ω) / ω) (c_t / y_n)^{η + 1} \quad \text{with} \quad c_t := (1 + r) b + y_t - b' \]

We see that the planner internalizes the impact of the savings choice \(b'\) on the price of nontradables and hence the credit constraint.

Our first function returns the (unmaximized) RHS of the Bellman equation.

@jax.jit
def planner_T_generator(v, model, i_b, i_y_t, i_y_n, i_bp):
    """
    Given current state (b, y_t, y_n) with indices (i_b, i_y_t, i_y_n),
    compute the unmaximized right hand side (RHS) of the Bellman equation as a
    function of the next period choice bp = b'.  
    """
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    y_t = y_t_nodes[i_y_t]
    y_n = y_n_nodes[i_y_n]
    b, bp = b_grid[i_b], b_grid[i_bp]
    # Compute price of nontradables using aggregates
    c = (1 + r) * b + y_t - bp
    p = ((1 - ω) / ω) * (c / y_n)**(η + 1)
    # Compute household flow utility
    utility = w(model, c, y_n)
    # Compute expected value (continuation)
    EV = jnp.sum(v[i_bp, :, :] * Q[i_y_t, i_y_n, :, :])
    # Set up constraints and evaluate 
    credit_constraint_holds = - κ * (p * y_n + y_t) <= bp
    budget_constraint_holds = bp <= (1 + r) * b + y_t
    return jnp.where(jnp.logical_and(credit_constraint_holds, 
                                     budget_constraint_holds), 
                     utility + β * EV,
                     -jnp.inf)

# Vectorize over the control bp and all the current states
planner_T_generator = jax.vmap(planner_T_generator,
        in_axes=(None, None, None, None, None, 0))
planner_T_generator = jax.vmap(planner_T_generator, 
        in_axes=(None, None, None, None, 0, None))
planner_T_generator = jax.vmap(planner_T_generator, 
        in_axes=(None, None, None, 0, None, None))
planner_T_generator = jax.vmap(planner_T_generator, 
        in_axes=(None, None, 0, None, None, None))

Now we construct the Bellman operator.

@jax.jit
def planner_T(model, v):
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    b_size, y_size = len(b_grid), len(y_t_nodes)
    b_indices, y_indices = jnp.arange(b_size), jnp.arange(y_size)
    # Evaluate RHS of Bellman equation at all states and actions
    val = planner_T_generator(v, model,
                     b_indices, y_indices, y_indices, b_indices)
    # Maximize over bp
    return jnp.max(val, axis=-1)

Here’s a function that computes a greedy policy (best response to \(v\)).

@jax.jit
def planner_get_greedy(model, v):
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    b_size, y_size = len(b_grid), len(y_t_nodes)
    b_indices, y_indices = jnp.arange(b_size), jnp.arange(y_size)
    # Evaluate RHS of Bellman equation at all states and actions
    val = planner_T_generator(v, model,
                     b_indices, y_indices, y_indices, b_indices)
    # Maximize over bp
    return jnp.argmax(val, axis=-1)

def vfi(T, v_init, max_iter=10_000, tol=1e-5):
    """
    Use successive approximation to compute the fixed point of T, starting from
    v_init.

    """
    v = v_init

    def cond_fun(state):
        error, i, v = state
        return (error > tol) & (i < max_iter)
    
    def body_fun(state):
        error, i, v = state
        v_new = T(v)
        error = jnp.max(jnp.abs(v_new - v))
        return error, i+1, v_new

    error, i, v_new = jax.lax.while_loop(cond_fun, body_fun,
                                                    (tol+1, 0, v))
    return v_new, i

vfi = jax.jit(vfi, static_argnums=(0,))

Computing the planner solution is straightforward value function iteration:

def compute_planner_solution(model):
    """
    Compute the constrained planner solution.

    """
    σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
    b_size, y_size = len(b_grid), len(y_t_nodes)
    b_indices = jnp.arange(b_size)
    v_init = jnp.ones((b_size, y_size, y_size))
    _T = lambda v: planner_T(model, v)
    # Compute household response to current guess H
    v, vfi_num_iter = vfi(_T, v_init)
    bp_policy = planner_get_greedy(model, v)
    return v, bp_policy, vfi_num_iter

20.5. Numerical solution#

Let’s now solve the model and compare the decentralized and planner solutions

20.5.1. Generating solutions#

Here we compute the two solutions.

model = create_overborrowing_model()
σ, η, β, ω, κ, r, b_grid, y_t_nodes, y_n_nodes, Q = model
b_size, y_size = len(b_grid), len(y_t_nodes)

print("Computing decentralized solution.")
in_time = time.time()
H_eq = compute_equilibrium(model)
out_time = time.time()
diff = out_time - in_time
print(f"Computed decentralized equilibrium in {diff} seconds")

Computing decentralized solution.

Updated H at iteration 0 with error 0.4094868302345276.

Updated H at iteration 1 with error 0.08928662538528442.

Updated H at iteration 2 with error 0.13957446813583374.

Updated H at iteration 3 with error 0.11391741037368774.

Updated H at iteration 4 with error 0.06260326504707336.

Updated H at iteration 5 with error 0.05131411552429199.

Updated H at iteration 6 with error 0.043103933334350586.

Updated H at iteration 7 with error 0.03797250986099243.

Updated H at iteration 8 with error 0.0328410267829895.

Updated H at iteration 9 with error 0.0287359356880188.

Updated H at iteration 10 with error 0.024630755186080933.

Updated H at iteration 11 with error 0.020525693893432617.

Updated H at iteration 12 with error 0.01744687557220459.

Updated H at iteration 13 with error 0.015394270420074463.

Updated H at iteration 14 with error 0.012315452098846436.

Updated H at iteration 15 with error 0.011289149522781372.

Updated H at iteration 16 with error 0.009236574172973633.

Updated H at iteration 17 with error 0.008210301399230957.

Updated H at iteration 18 with error 0.0071839988231658936.

Updated H at iteration 19 with error 0.00615769624710083.

Updated H at iteration 20 with error 0.00513148307800293.

Updated H at iteration 21 with error 0.005131423473358154.

Updated H at iteration 22 with error 0.0041051506996154785.
Computed decentralized equilibrium in 12.149990797042847 seconds

print("Computing planner's solution.")
in_time = time.time()
planner_v, H_plan, vfi_num_iter = compute_planner_solution(model)
out_time = time.time()
diff = out_time - in_time
print(f"Computed planner's solution in {diff} seconds")

Computing planner's solution.

Computed planner's solution in 0.9841585159301758 seconds

20.5.2. Policy plots#

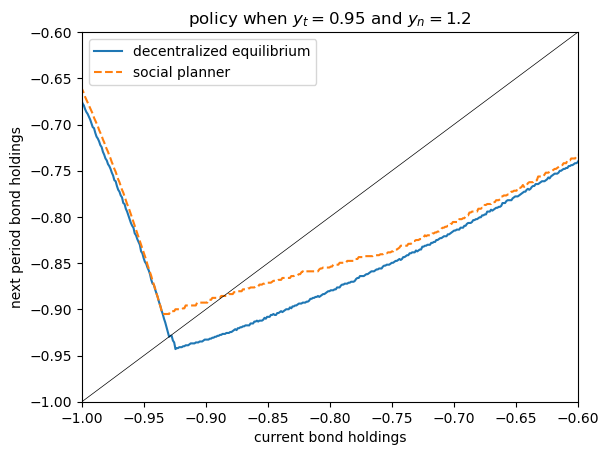
We produce a policy plot that is similar to Figure 1 in Bianchi (2011).

i, j = 1, 3
y_t, y_n = y_t_nodes[i], y_n_nodes[j]
fig, ax = plt.subplots()
ax.plot(b_grid, b_grid[H_eq[:, i, j]], label='decentralized equilibrium')
ax.plot(b_grid, b_grid[H_plan[:, i, j]], ls='--', label='social planner')
ax.plot(b_grid, b_grid, color='black', lw=0.5)
ax.set_ylim((-1.0, -0.6))
ax.set_xlim((-1.0, -0.6))
ax.set_xlabel("current bond holdings")
ax.set_ylabel("next period bond holdings")
ax.set_title(f"policy when $y_t = {y_t:.2}$ and $y_n = {y_n:.2}$")
ax.legend()
plt.show()
_images/0663678ef213b2902fc91ae0b9d0a70dd8908e51ab5828ea7a3b30fd31a06666.png

The match is not exact because we use a different estimate of the Markov dynamics for income.

Nonetheless, it is qualitatively similar.

20.6. Exercise#

Exercise 20.1

Your task is to examine the ergodic distribution of borrowing in the decentralized and planner equilibria.

We recommend that you use simulation and a kernel density estimate.

Here’s a function for generating the borrowing sequence.

We use Numba because we want to compile a long for loop.

@numba.jit
def generate_borrowing_sequence(H, y_t_series, y_n_series):
    """
    Generate the borrowing sequence B' = H(B, y_t, y_n).

    * H is a policy array
    * y_t_series and y_n_series are simulated time paths 

    Both y_t_series and y_n_series are stored as indices rather than values.

    """
    B = np.empty_like(y_t_series)
    B[0] = 0
    for t in range(len(y_t_series)-1):
        B[t+1] = H[B[t], y_t_series[t], y_n_series[t]]
    return B

Note that you will have to convert JAX arrays into NumPy arrays if you want to use this function.

From here you will need to

  • generate a time path for income \(y = (y_t, y_n)\) using one of the functions provided above.

  • use the function generate_borrowing_sequence plus H_eq and H_plan to calculate bond holdings for the planner and the decentralized equilibrium

  • produce a kernel density plot for each of these data sets

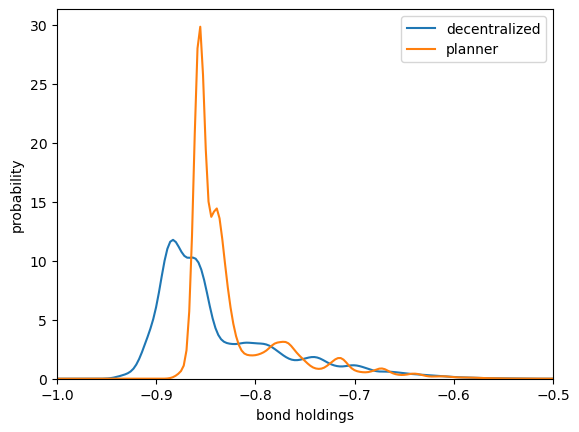
If you are successful, your plot should look something like Fig 2 of Bianchi (2011) — although not exactly the same, due to the alternative specification of the Markov process.

To generate a kernel density plot, we recommend that you use kdeplot from the package seaborn, which is included in Anaconda.