14. Optimal Investment#
GPU
This lecture was built using a machine with access to a GPU.
Google Colab has a free tier with GPUs that you can access as follows:
Click on the “play” icon top right
Select Colab
Set the runtime environment to include a GPU
In addition to JAX and Anaconda, this lecture will need the following libraries:
!pip install --upgrade quantecon
We study a monopolist who faces inverse demand curve
\[
P_t = a_0 - a_1 Y_t + Z_t,
\]
where
\(P_t\) is price,
\(Y_t\) is output and
\(Z_t\) is a demand shock.
We assume that \(Z_t\) is a discretized AR(1) process, specified below.
Current profits are
\[ P_t Y_t - c Y_t - \gamma (Y_{t+1} - Y_t)^2 \]
Combining with the demand curve and writing \(y, y'\) for \(Y_t, Y_{t+1}\), this becomes
\[ r(y, z, y') := (a_0 - a_1 y + z - c) y - γ (y' - y)^2 \]
The firm maximizes present value of expected discounted profits. The Bellman equation is
\[ v(y, z) = \max_{y'} \left\{ r(y, z, y') + β \sum_{z'} v(y', z') Q(z, z') \right\}. \]
We discretize \(y\) to a finite grid y_grid.
In essence, the firm tries to choose output close to the monopolist profit maximizer, given \(Z_t\), but is constrained by adjustment costs.
Let’s begin with the following imports
import quantecon as qe
import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
from time import time
Let’s check the GPU we are running
!nvidia-smi
Mon Dec 8 03:48:29 2025
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 580.105.08 Driver Version: 580.105.08 CUDA Version: 13.0 |
+-----------------------------------------+------------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+========================+======================|
| 0 Tesla T4 On | 00000000:00:1E.0 Off | 0 |
| N/A 28C P8 9W / 70W | 0MiB / 15360MiB | 0% Default |
| | | N/A |
+-----------------------------------------+------------------------+----------------------+
+-----------------------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=========================================================================================|
| No running processes found |
+-----------------------------------------------------------------------------------------+
We will use 64 bit floats with JAX in order to increase the precision.
jax.config.update("jax_enable_x64", True)
Let’s define a function to create an investment model using the given parameters.
def create_investment_model(
r=0.01, # Interest rate
a_0=10.0, a_1=1.0, # Demand parameters
γ=25.0, c=1.0, # Adjustment and unit cost
y_min=0.0, y_max=20.0, y_size=100, # Grid for output
ρ=0.9, ν=1.0, # AR(1) parameters
z_size=150): # Grid size for shock
"""
A function that takes in parameters and returns an instance of Model that
contains data for the investment problem.
"""
β = 1 / (1 + r)
y_grid = jnp.linspace(y_min, y_max, y_size)
mc = qe.tauchen(z_size, ρ, ν)
z_grid, Q = mc.state_values, mc.P
# Break up parameters into static and nonstatic components
constants = β, a_0, a_1, γ, c
sizes = y_size, z_size
arrays = y_grid, z_grid, Q
# Shift arrays to the device (e.g., GPU)
arrays = tuple(map(jax.device_put, arrays))
return constants, sizes, arrays
Let’s re-write the vectorized version of the right-hand side of the Bellman equation (before maximization), which is a 3D array representing
\[
B(y, z, y') = r(y, z, y') + \beta \sum_{z'} v(y', z') Q(z, z')
\]
for all \((y, z, y')\).
def B(v, constants, sizes, arrays):
"""
A vectorized version of the right-hand side of the Bellman equation
(before maximization)
"""
# Unpack
β, a_0, a_1, γ, c = constants
y_size, z_size = sizes
y_grid, z_grid, Q = arrays
# Compute current rewards r(y, z, yp) as array r[i, j, ip]
y = jnp.reshape(y_grid, (y_size, 1, 1)) # y[i] -> y[i, j, ip]
z = jnp.reshape(z_grid, (1, z_size, 1)) # z[j] -> z[i, j, ip]
yp = jnp.reshape(y_grid, (1, 1, y_size)) # yp[ip] -> yp[i, j, ip]
r = (a_0 - a_1 * y + z - c) * y - γ * (yp - y)**2
# Calculate continuation rewards at all combinations of (y, z, yp)
v = jnp.reshape(v, (1, 1, y_size, z_size)) # v[ip, jp] -> v[i, j, ip, jp]
Q = jnp.reshape(Q, (1, z_size, 1, z_size)) # Q[j, jp] -> Q[i, j, ip, jp]
EV = jnp.sum(v * Q, axis=3) # sum over last index jp
# Compute the right-hand side of the Bellman equation
return r + β * EV
# Create a jitted function
B = jax.jit(B, static_argnums=(2,))
We define a function to compute the current rewards \(r_\sigma\) given policy \(\sigma\), which is defined as the vector
\[ r_\sigma(y, z) := r(y, z, \sigma(y, z)) \]
def compute_r_σ(σ, constants, sizes, arrays):
"""
Compute the array r_σ[i, j] = r[i, j, σ[i, j]], which gives current
rewards given policy σ.
"""
# Unpack model
β, a_0, a_1, γ, c = constants
y_size, z_size = sizes
y_grid, z_grid, Q = arrays
# Compute r_σ[i, j]
y = jnp.reshape(y_grid, (y_size, 1))
z = jnp.reshape(z_grid, (1, z_size))
yp = y_grid[σ]
r_σ = (a_0 - a_1 * y + z - c) * y - γ * (yp - y)**2
return r_σ
# Create the jitted function
compute_r_σ = jax.jit(compute_r_σ, static_argnums=(2,))
Define the Bellman operator.
def T(v, constants, sizes, arrays):
"""The Bellman operator."""
return jnp.max(B(v, constants, sizes, arrays), axis=2)
T = jax.jit(T, static_argnums=(2,))
The following function computes a v-greedy policy.
def get_greedy(v, constants, sizes, arrays):
"Computes a v-greedy policy, returned as a set of indices."
return jnp.argmax(B(v, constants, sizes, arrays), axis=2)
get_greedy = jax.jit(get_greedy, static_argnums=(2,))
Define the \(\sigma\)-policy operator.
def T_σ(v, σ, constants, sizes, arrays):
"""The σ-policy operator."""
# Unpack model
β, a_0, a_1, γ, c = constants
y_size, z_size = sizes
y_grid, z_grid, Q = arrays
r_σ = compute_r_σ(σ, constants, sizes, arrays)
# Compute the array v[σ[i, j], jp]
zp_idx = jnp.arange(z_size)
zp_idx = jnp.reshape(zp_idx, (1, 1, z_size))
σ = jnp.reshape(σ, (y_size, z_size, 1))
V = v[σ, zp_idx]
# Convert Q[j, jp] to Q[i, j, jp]
Q = jnp.reshape(Q, (1, z_size, z_size))
# Calculate the expected sum Σ_jp v[σ[i, j], jp] * Q[i, j, jp]
Ev = jnp.sum(V * Q, axis=2)
return r_σ + β * Ev
T_σ = jax.jit(T_σ, static_argnums=(3,))
Next, we want to computes the lifetime value of following policy \(\sigma\).
This lifetime value is a function \(v_\sigma\) that satisfies
\[ v_\sigma(y, z) = r_\sigma(y, z) + \beta \sum_{z'} v_\sigma(\sigma(y, z), z') Q(z, z') \]
We wish to solve this equation for \(v_\sigma\).
Suppose we define the linear operator \(L_\sigma\) by
\[ (L_\sigma v)(y, z) = v(y, z) - \beta \sum_{z'} v(\sigma(y, z), z') Q(z, z') \]
With this notation, the problem is to solve for \(v\) via
\[
(L_{\sigma} v)(y, z) = r_\sigma(y, z)
\]
In vector for this is \(L_\sigma v = r_\sigma\), which tells us that the function we seek is
\[ v_\sigma = L_\sigma^{-1} r_\sigma \]
JAX allows us to solve linear systems defined in terms of operators; the first step is to define the function \(L_{\sigma}\).
def L_σ(v, σ, constants, sizes, arrays):
β, a_0, a_1, γ, c = constants
y_size, z_size = sizes
y_grid, z_grid, Q = arrays
# Set up the array v[σ[i, j], jp]
zp_idx = jnp.arange(z_size)
zp_idx = jnp.reshape(zp_idx, (1, 1, z_size))
σ = jnp.reshape(σ, (y_size, z_size, 1))
V = v[σ, zp_idx]
# Expand Q[j, jp] to Q[i, j, jp]
Q = jnp.reshape(Q, (1, z_size, z_size))
# Compute and return v[i, j] - β Σ_jp v[σ[i, j], jp] * Q[j, jp]
return v - β * jnp.sum(V * Q, axis=2)
L_σ = jax.jit(L_σ, static_argnums=(3,))
Now we can define a function to compute \(v_{\sigma}\)
def get_value(σ, constants, sizes, arrays):
# Unpack
β, a_0, a_1, γ, c = constants
y_size, z_size = sizes
y_grid, z_grid, Q = arrays
r_σ = compute_r_σ(σ, constants, sizes, arrays)
# Reduce L_σ to a function in v
partial_L_σ = lambda v: L_σ(v, σ, constants, sizes, arrays)
return jax.scipy.sparse.linalg.bicgstab(partial_L_σ, r_σ)[0]
get_value = jax.jit(get_value, static_argnums=(2,))
We use successive approximation for VFI.
def successive_approx_jax(T, # Operator (callable)
x_0, # Initial condition
tol=1e-6, # Error tolerance
max_iter=10_000): # Max iteration bound
def body_fun(k_x_err):
k, x, error = k_x_err
x_new = T(x)
error = jnp.max(jnp.abs(x_new - x))
return k + 1, x_new, error
def cond_fun(k_x_err):
k, x, error = k_x_err
return jnp.logical_and(error > tol, k < max_iter)
k, x, error = jax.lax.while_loop(cond_fun, body_fun, (1, x_0, tol + 1))
return x
successive_approx_jax = jax.jit(successive_approx_jax, static_argnums=(0,))
For OPI we’ll add a compiled routine that computes \(T_σ^m v\).
def iterate_policy_operator(σ, v, m, params, sizes, arrays):
def update(i, v):
v = T_σ(v, σ, params, sizes, arrays)
return v
v = jax.lax.fori_loop(0, m, update, v)
return v
iterate_policy_operator = jax.jit(iterate_policy_operator,
static_argnums=(4,))
Finally, we introduce the solvers that implement VFI, HPI and OPI.
def value_function_iteration(model, tol=1e-5):
"""
Implements value function iteration.
"""
params, sizes, arrays = model
vz = jnp.zeros(sizes)
_T = lambda v: T(v, params, sizes, arrays)
v_star = successive_approx_jax(_T, vz, tol=tol)
return get_greedy(v_star, params, sizes, arrays)
For OPI we will use a compiled JAX lax.while_loop operation to speed execution.
def opi_loop(params, sizes, arrays, m, tol, max_iter):
"""
Implements optimistic policy iteration (see dp.quantecon.org) with
step size m.
"""
v_init = jnp.zeros(sizes)
def condition_function(inputs):
i, v, error = inputs
return jnp.logical_and(error > tol, i < max_iter)
def update(inputs):
i, v, error = inputs
last_v = v
σ = get_greedy(v, params, sizes, arrays)
v = iterate_policy_operator(σ, v, m, params, sizes, arrays)
error = jnp.max(jnp.abs(v - last_v))
i += 1
return i, v, error
num_iter, v, error = jax.lax.while_loop(condition_function,
update,
(0, v_init, tol + 1))
return get_greedy(v, params, sizes, arrays)
opi_loop = jax.jit(opi_loop, static_argnums=(1,))
Here’s a friendly interface to OPI
def optimistic_policy_iteration(model, m=10, tol=1e-5, max_iter=10_000):
params, sizes, arrays = model
σ_star = opi_loop(params, sizes, arrays, m, tol, max_iter)
return σ_star
Here’s HPI
def howard_policy_iteration(model, maxiter=250):
"""
Implements Howard policy iteration (see dp.quantecon.org)
"""
params, sizes, arrays = model
σ = jnp.zeros(sizes, dtype=int)
i, error = 0, 1.0
while error > 0 and i < maxiter:
v_σ = get_value(σ, params, sizes, arrays)
σ_new = get_greedy(v_σ, params, sizes, arrays)
error = jnp.max(jnp.abs(σ_new - σ))
σ = σ_new
i = i + 1
print(f"Concluded loop {i} with error {error}.")
return σ
model = create_investment_model()
constants, sizes, arrays = model
β, a_0, a_1, γ, c = constants
y_size, z_size = sizes
y_grid, z_grid, Q = arrays
print("Starting HPI.")
%time σ_star_hpi = howard_policy_iteration(model).block_until_ready()
# Now time it without compile time
start = time()
σ_star_hpi = howard_policy_iteration(model).block_until_ready()
hpi_without_compile = time() - start
print(σ_star_hpi)
print(f"HPI completed in {hpi_without_compile} seconds.")
Concluded loop 1 with error 50.
Concluded loop 2 with error 26.
Concluded loop 3 with error 17.
Concluded loop 4 with error 10.
Concluded loop 5 with error 7.
Concluded loop 6 with error 4.
Concluded loop 7 with error 3.
Concluded loop 8 with error 1.
Concluded loop 9 with error 1.
Concluded loop 10 with error 1.
Concluded loop 11 with error 1.
Concluded loop 12 with error 0.
[[ 2 2 2 ... 6 6 6]
[ 3 3 3 ... 7 7 7]
[ 4 4 4 ... 7 7 7]
...
[82 82 82 ... 86 86 86]
[83 83 83 ... 86 86 86]
[84 84 84 ... 87 87 87]]
HPI completed in 0.11741876602172852 seconds.
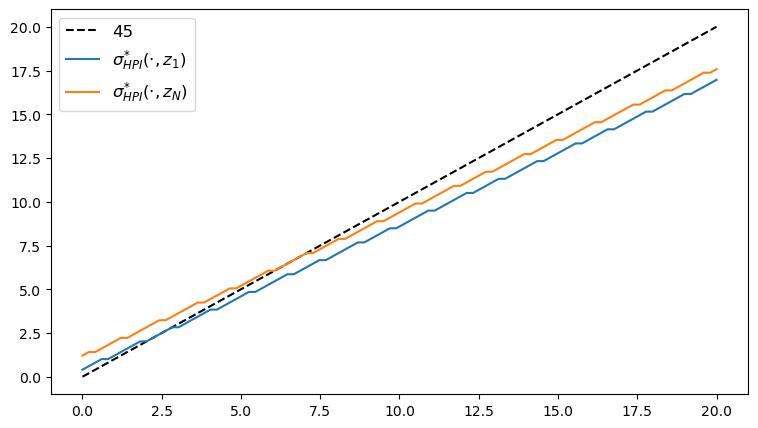
Here’s the plot of the Howard policy, as a function of \(y\) at the highest and lowest values of \(z\).
fig, ax = plt.subplots(figsize=(9, 5))
ax.plot(y_grid, y_grid, "k--", label="45")
ax.plot(y_grid, y_grid[σ_star_hpi[:, 1]], label="$\\sigma^{*}_{HPI}(\cdot, z_1)$")
ax.plot(y_grid, y_grid[σ_star_hpi[:, -1]], label="$\\sigma^{*}_{HPI}(\cdot, z_N)$")
ax.legend(fontsize=12)
plt.show()
print("Starting VFI.")
%time σ_star_vfi = value_function_iteration(model).block_until_ready()
# Now time it without compile time
start = time()
σ_star_vfi = value_function_iteration(model).block_until_ready()
vfi_without_compile = time() - start
print(σ_star_vfi)
print(f"VFI completed in {vfi_without_compile} seconds.")
[[ 2 2 2 ... 6 6 6]
[ 3 3 3 ... 7 7 7]
[ 4 4 4 ... 7 7 7]
...
[82 82 82 ... 86 86 86]
[83 83 83 ... 86 86 86]
[84 84 84 ... 87 87 87]]
VFI completed in 0.7327821254730225 seconds.
Here’s the plot of the VFI, as a function of \(y\) at the highest and lowest values of \(z\).
fig, ax = plt.subplots(figsize=(9, 5))
ax.plot(y_grid, y_grid, "k--", label="45")
ax.plot(y_grid, y_grid[σ_star_vfi[:, 1]], label="$\\sigma^{*}_{VFI}(\cdot, z_1)$")
ax.plot(y_grid, y_grid[σ_star_vfi[:, -1]], label="$\\sigma^{*}_{VFI}(\cdot, z_N)$")
ax.legend(fontsize=12)
plt.show()
print("Starting OPI.")
%time σ_star_opi = optimistic_policy_iteration(model, m=100).block_until_ready()
# Now time it without compile time
start = time()
σ_star_opi = optimistic_policy_iteration(model, m=100).block_until_ready()
opi_without_compile = time() - start
print(σ_star_opi)
print(f"OPI completed in {opi_without_compile} seconds.")
[[ 2 2 2 ... 6 6 6]
[ 3 3 3 ... 7 7 7]
[ 4 4 4 ... 7 7 7]
...
[82 82 82 ... 86 86 86]
[83 83 83 ... 86 86 86]
[84 84 84 ... 87 87 87]]
OPI completed in 0.20464134216308594 seconds.
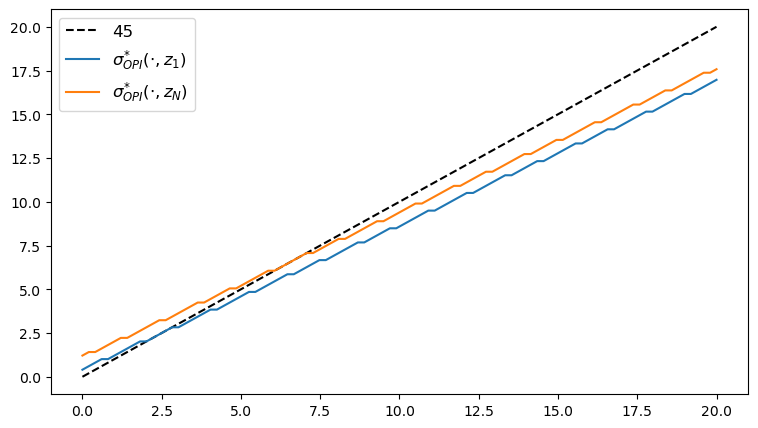
Here’s the plot of the optimal policy, as a function of \(y\) at the highest and lowest values of \(z\).
fig, ax = plt.subplots(figsize=(9, 5))
ax.plot(y_grid, y_grid, "k--", label="45")
ax.plot(y_grid, y_grid[σ_star_opi[:, 1]], label="$\\sigma^{*}_{OPI}(\cdot, z_1)$")
ax.plot(y_grid, y_grid[σ_star_opi[:, -1]], label="$\\sigma^{*}_{OPI}(\cdot, z_N)$")
ax.legend(fontsize=12)
plt.show()
We observe that all the solvers produce the same output from the above three plots.
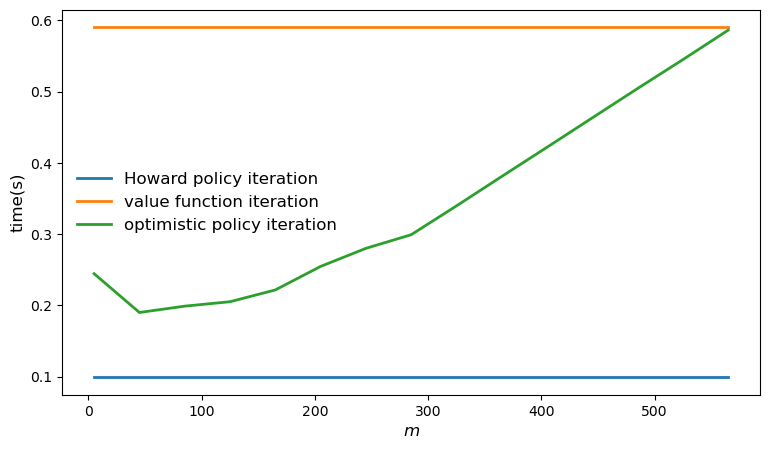
Let’s plot the time taken by each of the solvers and compare them.
m_vals = range(5, 600, 40)
print("Running Howard policy iteration.")
%time σ_hpi = howard_policy_iteration(model).block_until_ready()
Running Howard policy iteration.
Concluded loop 1 with error 50.
Concluded loop 2 with error 26.
Concluded loop 3 with error 17.
Concluded loop 4 with error 10.
Concluded loop 5 with error 7.
Concluded loop 6 with error 4.
Concluded loop 7 with error 3.
Concluded loop 8 with error 1.
Concluded loop 9 with error 1.
Concluded loop 10 with error 1.
Concluded loop 11 with error 1.
Concluded loop 12 with error 0.
CPU times: user 111 ms, sys: 8.39 ms, total: 119 ms
Wall time: 99.4 ms
# Now time it without compile time
start = time()
σ_hpi = howard_policy_iteration(model).block_until_ready()
hpi_without_compile = time() - start
print(f"HPI completed in {hpi_without_compile} seconds.")
Concluded loop 1 with error 50.
Concluded loop 2 with error 26.
Concluded loop 3 with error 17.
Concluded loop 4 with error 10.
Concluded loop 5 with error 7.
Concluded loop 6 with error 4.
Concluded loop 7 with error 3.
Concluded loop 8 with error 1.
Concluded loop 9 with error 1.
Concluded loop 10 with error 1.
Concluded loop 11 with error 1.
Concluded loop 12 with error 0.
HPI completed in 0.09869885444641113 seconds.
print("Running value function iteration.")
%time σ_vfi = value_function_iteration(model, tol=1e-5).block_until_ready()
Running value function iteration.
CPU times: user 525 ms, sys: 3.67 ms, total: 529 ms
Wall time: 583 ms
# Now time it without compile time
start = time()
σ_vfi = value_function_iteration(model, tol=1e-5).block_until_ready()
vfi_without_compile = time() - start
print(f"VFI completed in {vfi_without_compile} seconds.")
VFI completed in 0.5863316059112549 seconds.
opi_times = []
for m in m_vals:
print(f"Running optimistic policy iteration with m={m}.")
σ_opi = optimistic_policy_iteration(model, m=m, tol=1e-5).block_until_ready()
# Now time it without compile time
start = time()
σ_opi = optimistic_policy_iteration(model, m=m, tol=1e-5).block_until_ready()
opi_without_compile = time() - start
print(f"OPI with m={m} completed in {opi_without_compile} seconds.")
opi_times.append(opi_without_compile)
fig, ax = plt.subplots(figsize=(9, 5))
ax.plot(m_vals, jnp.full(len(m_vals), hpi_without_compile),
lw=2, label="Howard policy iteration")
ax.plot(m_vals, jnp.full(len(m_vals), vfi_without_compile),
lw=2, label="value function iteration")
ax.plot(m_vals, opi_times, lw=2, label="optimistic policy iteration")
ax.legend(fontsize=12, frameon=False)
ax.set_xlabel("$m$", fontsize=12)
ax.set_ylabel("time(s)", fontsize=12)
plt.show()
