4. Newton’s Method via JAX#

GPU

This lecture was built using a machine with JAX installed and access to a GPU.

To run this lecture on Google Colab, click on the “play” icon top right, select Colab, and set the runtime environment to include a GPU.

To run this lecture on your own machine, you need to install Google JAX.

4.1. Overview#

One of the key features of JAX is automatic differentiation.

We introduced this feature in Adventures with Autodiff.

In this lecture we apply automatic differentiation to the problem of computing economic equilibria via Newton’s method.

Newton’s method is a relatively simple root and fixed point solution algorithm, which we discussed in a more elementary QuantEcon lecture.

JAX is ideally suited to implementing Newton’s method efficiently, even in high dimensions.

We use the following imports in this lecture

import jax
import jax.numpy as jnp
from scipy.optimize import root
import matplotlib.pyplot as plt

Let’s check the GPU we are running

!nvidia-smi

Wed Nov 20 00:33:02 2024       
+---------------------------------------------------------------------------------------+
| NVIDIA-SMI 535.54.03              Driver Version: 535.54.03    CUDA Version: 12.6     |
|-----------------------------------------+----------------------+----------------------+
| GPU  Name                 Persistence-M | Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp   Perf          Pwr:Usage/Cap |         Memory-Usage | GPU-Util  Compute M. |
|                                         |                      |               MIG M. |
|=========================================+======================+======================|
|   0  Tesla T4                       On  | 00000001:00:00.0 Off |                    0 |
| N/A   45C    P0              28W /  70W |      2MiB / 15360MiB |      0%      Default |
|                                         |                      |                  N/A |
+-----------------------------------------+----------------------+----------------------+
                                                                                         
+---------------------------------------------------------------------------------------+
| Processes:                                                                            |
|  GPU   GI   CI        PID   Type   Process name                            GPU Memory |
|        ID   ID                                                             Usage      |
|=======================================================================================|
|  No running processes found                                                           |
+---------------------------------------------------------------------------------------+

4.2. Newton in one dimension#

As a warm up, let’s implement Newton’s method in JAX for a simple one-dimensional root-finding problem.

Let \(f\) be a function from \(\mathbb R\) to itself.

A root of \(f\) is an \(x \in \mathbb R\) such that \(f(x)=0\).

Recall that Newton’s method for solving for the root of \(f\) involves iterating with the map \(q\) defined by

\[ q(x) = x - \frac{f(x)}{f'(x)} \]

Here is a function called newton that takes a function \(f\) plus a scalar value \(x_0\), iterates with \(q\) starting from \(x_0\), and returns an approximate fixed point.

def newton(f, x_0, tol=1e-5):
    f_prime = jax.grad(f)
    def q(x):
        return x - f(x) / f_prime(x)

    error = tol + 1
    x = x_0
    while error > tol:
        y = q(x)
        error = abs(x - y)
        x = y
        
    return x

The code above uses automatic differentiation to calculate \(f'\) via the call to jax.grad.

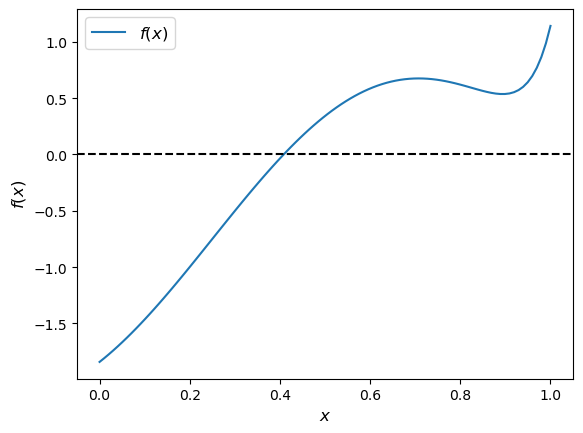
Let’s test our newton routine on the function shown below.

f = lambda x: jnp.sin(4 * (x - 1/4)) + x + x**20 - 1
x = jnp.linspace(0, 1, 100)

fig, ax = plt.subplots()
ax.plot(x, f(x), label='$f(x)$')
ax.axhline(ls='--', c='k')
ax.set_xlabel('$x$', fontsize=12)
ax.set_ylabel('$f(x)$', fontsize=12)
ax.legend(fontsize=12)
plt.show()
_images/0ab129c096d268f4e08a844d52a9c59f123b0a676523a3c5ade85e22c2c4f9d9.png

Here we go

newton(f, 0.2)

Array(0.4082935, dtype=float32, weak_type=True)

This number looks to be close to the root, given the figure.

4.3. An Equilibrium Problem#

Now let’s move up to higher dimensions.

First we describe a market equilibrium problem we will solve with JAX via root-finding.

The market is for \(n\) goods.

(We are extending a two-good version of the market from an earlier lecture.)

The supply function for the \(i\)-th good is

\[ q^s_i (p) = b_i \sqrt{p_i} \]

which we write in vector form as

\[ q^s (p) =b \sqrt{p} \]

(Here \(\sqrt{p}\) is the square root of each \(p_i\) and \(b \sqrt{p}\) is the vector formed by taking the pointwise product \(b_i \sqrt{p_i}\) at each \(i\).)

The demand function is

\[ q^d (p) = \exp(- A p) + c \]

(Here \(A\) is an \(n \times n\) matrix containing parameters, \(c\) is an \(n \times 1\) vector and the \(\exp\) function acts pointwise (element-by-element) on the vector \(- A p\).)

The excess demand function is

\[ e(p) = \exp(- A p) + c - b \sqrt{p} \]

An equilibrium price vector is an \(n\)-vector \(p\) such that \(e(p) = 0\).

The function below calculates the excess demand for given parameters

def e(p, A, b, c):
    return jnp.exp(- A @ p) + c - b * jnp.sqrt(p)

4.4. Computation#

In this section we describe and then implement the solution method.

4.4.1. Newton’s Method#

We use a multivariate version of Newton’s method to compute the equilibrium price.

The rule for updating a guess \(p_n\) of the equilibrium price vector is

(4.1)#\[p_{n+1} = p_n - J_e(p_n)^{-1} e(p_n)\]

Here \(J_e(p_n)\) is the Jacobian of \(e\) evaluated at \(p_n\).

Iteration starts from initial guess \(p_0\).

Instead of coding the Jacobian by hand, we use automatic differentiation via jax.jacobian().

def newton(f, x_0, tol=1e-5, max_iter=15):
    """
    A multivariate Newton root-finding routine.

    """
    x = x_0
    f_jac = jax.jacobian(f)
    @jax.jit
    def q(x):
        " Updates the current guess. "
        return x - jnp.linalg.solve(f_jac(x), f(x))
    error = tol + 1
    n = 0
    while error > tol:
        n += 1
        if(n > max_iter):
            raise Exception('Max iteration reached without convergence')
        y = q(x)
        error = jnp.linalg.norm(x - y)
        x = y
        print(f'iteration {n}, error = {error}')
    return x

4.4.2. Application#

Let’s now apply the method just described to investigate a large market with 5,000 goods.

We randomly generate the matrix \(A\) and set the parameter vectors \(b, c\) to \(1\).

dim = 5_000
seed = 32

# Create a random matrix A and normalize the rows to sum to one
key = jax.random.PRNGKey(seed)
A = jax.random.uniform(key, [dim, dim])
s = jnp.sum(A, axis=0)
A = A / s

# Set up b and c
b = jnp.ones(dim)
c = jnp.ones(dim)

Here’s our initial condition \(p_0\)

init_p = jnp.ones(dim)

By combining the power of Newton’s method, JAX accelerated linear algebra, automatic differentiation, and a GPU, we obtain a relatively small error for this high-dimensional problem in just a few seconds:

%%time
p = newton(lambda p: e(p, A, b, c), init_p).block_until_ready()

iteration 1, error = 29.977458953857422
iteration 2, error = 5.092828750610352
iteration 3, error = 0.10971637070178986

iteration 4, error = 5.167595372768119e-05
iteration 5, error = 1.1732883649528958e-05
iteration 6, error = 4.191016159893479e-06
CPU times: user 5.45 s, sys: 520 ms, total: 5.97 s
Wall time: 5.85 s

We run it again to eliminate compile time.

%%time
p = newton(lambda p: e(p, A, b, c), init_p).block_until_ready()

iteration 1, error = 29.977458953857422
iteration 2, error = 5.092828750610352
iteration 3, error = 0.10971637070178986

iteration 4, error = 5.167595372768119e-05
iteration 5, error = 1.1732883649528958e-05
iteration 6, error = 4.191016159893479e-06
CPU times: user 1.56 s, sys: 337 ms, total: 1.9 s
Wall time: 1.8 s

Here’s the size of the error:

jnp.max(jnp.abs(e(p, A, b, c)))

Array(1.1920929e-07, dtype=float32)

With the same tolerance, SciPy’s root function takes much longer to run, even with the Jacobian supplied.

%%time
solution = root(lambda p: e(p, A, b, c),
                init_p,
                jac=lambda p: jax.jacobian(e)(p, A, b, c),
                method='hybr',
                tol=1e-5)

CPU times: user 1min 55s, sys: 148 ms, total: 1min 55s
Wall time: 1min 55s

The result is also slightly less accurate:

p = solution.x
jnp.max(jnp.abs(e(p, A, b, c)))

Array(8.34465e-07, dtype=float32)

4.5. Exercises#

Exercise 4.1

Consider a three-dimensional extension of the Solow fixed point problem with

\[\begin{split} A = \begin{pmatrix} 2 & 3 & 3 \\ 2 & 4 & 2 \\ 1 & 5 & 1 \\ \end{pmatrix}, \quad s = 0.2, \quad α = 0.5, \quad δ = 0.8 \end{split}\]

As before the law of motion is

\[ k_{t+1} = g(k_t) \quad \text{where} \quad g(k) := sAk^\alpha + (1-\delta) k\]

However \(k_t\) is now a \(3 \times 1\) vector.

Solve for the fixed point using Newton’s method with the following initial values:

\[\begin{split} \begin{aligned} k1_{0} &= (1, 1, 1) \\ k2_{0} &= (3, 5, 5) \\ k3_{0} &= (50, 50, 50) \end{aligned} \end{split}\]

Hint

  • The computation of the fixed point is equivalent to computing \(k^*\) such that \(f(k^*) - k^* = 0\).

  • If you are unsure about your solution, you can start with the solved example:

\[\begin{split}A = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{pmatrix}\end{split}\]

with \(s = 0.3\), \(α = 0.3\), and \(δ = 0.4\) and starting value:

\[k_0 = (1, 1, 1)\]

The result should converge to the analytical solution.

Exercise 4.2

In this exercise, let’s try different initial values and check how Newton’s method responds to different starting points.

Let’s define a three-good problem with the following default values:

\[\begin{split} A = \begin{pmatrix} 0.2 & 0.1 & 0.7 \\ 0.3 & 0.2 & 0.5 \\ 0.1 & 0.8 & 0.1 \\ \end{pmatrix}, \qquad b = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \qquad \text{and} \qquad c = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \end{split}\]

For this exercise, use the following extreme price vectors as initial values:

\[\begin{split}\begin{aligned} p1_{0} &= (5, 5, 5) \\ p2_{0} &= (1, 1, 1) \\ p3_{0} &= (4.5, 0.1, 4) \end{aligned} \end{split}\]

Set the tolerance to \(10^{-15}\) for more accurate output.

Hint

Similar to exercise 1, enabling float64 for JAX can improve the precision of our results.